Inscription / Connexion Nouveau Sujet
Oscillations mécaniques
Salut, j'ai eu des difficultés sur la dernière question de cet exercice.
Un solide S de masse m =200g est fixé à l'extrémité d'un ressort de raideur k 40N/m, de masse négligeable, à spires non jointives. L'autre extrémité du ressort est attachée à un support fixe. Le solide de masse m est guidé rectilignement sur un banc à coussin d'air horizontal. Les frottements sont négligeables. Le solide se déplace dans le repère (O,i) de X à X' . À la date t = 0, le solide S, en mouvement vers la position d'équilibre O dans le repère (O, i), passe par l'abscisse xo = -5 cm, avec une vitesse positive Vo 0,7 m.s¹.
1) Calculer:
a) l'énergie mécanique Em du système du système ressort- solide au début du mouvement;
b) la vitesse du solide au passage par la position d'équilibre;
c) le raccourcissement maximal du ressort;
d) la vitesse du solide au point d'abscisse x= 3,5 cm.
2) a) Etablir l'équation différentielle du mouvement du solide S.
b) Déterminer la pulsation, la période et la fréquence des oscillations.
c) Déterminer l'équation horaire du mouvement du centre d'inertie G du solide sous la forme x(t) = xmsin(wt + φ)
J'ai besoin de votre aide, merci !
Bonjour
Pour t'aider efficacement, il faudrait que tu expliques ce que tu as réussi à faire et ce qui te bloque. Pour la question 1), un raisonnement sur la conservation de l'énergie mécanique d'un système à définir est possible.
Voici ce que j'ai trouvé
1)a) Em=Ep+Ec=0,099J
b)V=√(2Em/m)=0,995m/s
c) Xm=√(2Em/k)=0,0703m
d)V=√((2Em-kx²)/m)=0,863m/s
2)a) En appliquant la RFD on obtient x''+(k/m)x=0
b) w=√(k/m)=14,14rad/s
T=(2π/w)=0,444s
f=(1/T)=2,25Hz
c) je n'arrive pas à trouver le déphasage Q
je n'arrive pas à trouver le déphasage
Connaissant l'expression générale de x(t), tu peux obtenir par dérivation l'expression générale de v(t). Ensuite l'énoncé fournit les valeurs de x et de v pour t=0...
Après dérivation et calcul pour t=0 j'obtiens sinQ=(xo/Xm) et cosQ=(Vo/wXm) en utilisant la tangente j'obtiens tanQ=-1,01 d'où Q=-0,79
La valeur d'une tangente ne fixe l'angle qu'à 
rad près. On obtient proprement le résultat en remarquant :
sin(
)<0 et cos()>0
Tu peux sans doute arrondir tan() à -1, ce qui permet simplement d'exprimer en radians en fonction de .
Aide-toi au besoin d'un cercle trigonométrique. Tu es sûr que les inégalités concernant le cosinus et le sinus sont vérifiées pour :
=/4 rad ?
Il faut se méfier de la fonction arctangente, en particulier quand le cosinus de l'angle est négatif, ce qui n'est pas le cas ici.
En attendant d'avoir étudié proprement la fonction arctangente,je te conseille comme déjà écrit d'utiliser un cercle trigonométrique.
Cela dit, puisque le cosinus est ici positif, ta calculatrice devrait te fournir le résultat. Mauvaise utilisation de ta part ?
le cosinus est positif et le sinus est négatif
Dans ces conditions, à quel intervalle de valeur appartient l'angle ? Utile un cercle trigonométrique si cela ne te parait pas évident !
Oui ! Tu devrais tout de même revoir ta trigonométrie. Petite question complémentaire si tu as le temps, pour illustrer les dangers potentiels de l'utilisation de la touche arctangente (tan-1 sur la plupart des calculatrices) ; imagine un autre problème qui aurait conduit à :
Que vaudrait ? Nous aurions toujours : tan()
-1...
Q=3π/4 mais pour Q=-π/4 il y a d'autres angles aussi qui vérifient le cosinus positif et le sinus négatif
Bonjour,
Le déphasage de deux signaux sinusoïdaux est un nombre quelconque, mais on le ramène généralement à l'intervalle ]-π ,+π].
Q=-π/4 il y a d'autres angles aussi qui vérifient le cosinus positif et le sinus négatif
Pour définir physiquement un angle, il faut connaître systématiquement une fonction trigonométrique de cet angle : la tangente par exemple mais, comme déjà écrit, cela ne suffit pas : il faut aussi connaître le signe d'une autre fonction.
Par exemple ici, il suffisait de savoir :
tan(
)=-1 et : cos()>0.
Maintenant, tu dois savoir en plus qu'un angle défini à partir de fonctions trigonométriques est défini modulo 2
. Si =-/4 convient, tous les angles vérifiant l'égalité suivante conviennent aussi :
=-/4+2k. où k est un entier relatif (voir cours de math).Je n'ai pas écrit cela. Il faut s'adapter au contexte. Pour déterminer exactement un angle ( éventuellement un déphasage mais pas seulement) il faut au minimum deux renseignements :
1 : la valeur d'une fonction trigonométrique de cet angle ;
2 : le signe d'une autre fonction trigonométrique de cet angle.
Ton énoncé fournit une valeur numérique non indispensable. La connaissance de xo permet de connaître sin(). Il aurait été suffisant alors de préciser que la vitesse initiale est positive,ce qui conduit à : cos()>0. Donner la valeur initiale de la vitesse n'est pas indispensable dans ce contexte. Pour bien comprendre, tu peux t'aider d'un cercle trigonométrique.
Ok compris, mais j'ai une autre préoccupation. Et si on demandait la date du 2e passage par la position d'équilibre ?
Il faudrait préciser le sens de la vitesse à ce passage à l'équilibre. Supposons qu'il soit positif. Les différentes dates de passage à l'équilibre avec vitesse positive sont les valeurs de t telles que :
sin(
t+)=0
et
cos (t+)>0.
Pas tout à fait. Un sinus nul correspond à un cosinus égal soit à zéro soit à -1. Il ne faut retenir que les solutions correspondant à un cosinus positif si tu t'intéresses aux passages à l'équilibre avec vitesse positive. Je me répète : "cercle trigonométrique" !
La courbe x=f(t) t'aidera peut-être à mieux comprendre mais il te faut avant tout bien revoir ton cours de math sur la trigonométrie.
L'axe des temps est gradué en huitièmes de période, ce qui est adapté dans ce cas où =-/4 rad
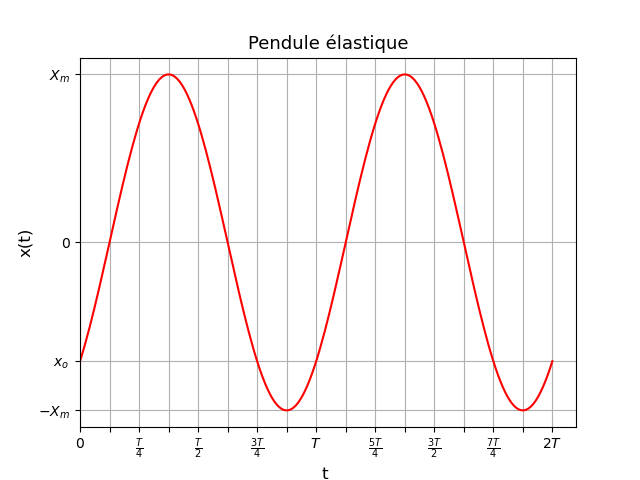
Il s'agit d'étudier le mouvement d'oscillations d'une masse de part et d'autre d'une position d'équilibre (x=0). Essaie de t'imaginer le mouvement... La masse passe en x=0 avec une vitesse positive, continue jusqu'à sa position extrême (x=Xm) pour repasser ensuite en x=0 avec une vitesse négative puis continue jusqu'en x=-Xm et ainsi de suite.
Le passage à l'équilibre dans un sens et le passage à l'équilibre dans l'autre sens sont deux situations physiques différentes. Il est normal de bien les distinguer...
Quelles sont les valeurs de (.t-/4) qui ont un sinus nul et un cosinus positif (cercle trigonométrique utile) ?
Essaie de fournir une réponse en fonction de T pour plus de généralités. Tu peux vérifier graphiquement ta réponse à l'aide de la courbe x=f(t) que je t'ai fournie.
Les solutions générales sont de la forme t=(5/8)T+kT ou t=(1/8)T+kT. Pour les solutions particulières, quelles sont les valeurs de k possibles ?
Le sinus est nul et le cosinus positif pour :
avec k entier relatif. Soit :
Si on exclut les valeurs de t négatives, k peut prendre les valeurs : 0, 1, 2, ... Donc les valeurs possibles de t sont :
Comme je me suis limité pour mon tracé à ,seules les deux premières valeurs apparaissent.
Un passage à l'équilibre avec vitesse négative correspondrait à un sinus nul et un cosinus négatif, donc à :
avec, pour t>0 : k=0, 1, 2, ... Seules les valeurs 5T/8 et 13T/8 apparaissent sur le tracé précédent.
Je comprends la résolution mais je n'ai pas compris la méthode. Pouvez me clarifier le concept de vitesse positive et négative pour la détermination des dates de passage (1er passage, 2e passage, 3e passage)?
Observe bien la courbe x=f(t) fournie précédemment. Les passages à l'équilibre correspondent à x=0.
Dans les cas : t=T/8, 9T/8... ce passage se fait avec x croissant en fonction de t donc avec une vitesse positive (n'oublie pas la signification de la dérivée v=dx/dt).
Dans les cas : t=5T/8, 13T/8... ce passage se fait avec x décroissant en fonction de t donc avec une vitesse négative.
si x=Xm.sin(t+)
v=dx/dt=Xm..cos(.t+)
On voit bien que le signe de la vitesse est le signe du cosinus.
Mais le sens de la vitesse dépend du mouvement non ? Quand le solide passe pour la première fois à la position d'équilibre avec une vitesse positive (respectivement négative) lors de son deuxième passage la vitesse sera négative (respectivement positive) si je comprends bien
Quand le solide passe pour la première fois à la position d'équilibre avec une vitesse positive (respectivement négative) lors de son deuxième passage la vitesse sera négative (respectivement positive) si je comprends bien
Oui. Le solide passe par la position d'équilibre toute les demies périodes, une fois dans un sens, la fois suivante dans le sens inverse et ainsi de suite. Observe bien la courbe x=f(t) fournie. Tu as une situation analogue avec un pendule (petite bille fixée à un point fixe à l'aide d'un fil) ou avec le balancier d'une horloge mécanique.
Je croyais que si on demandait de déterminer la date du 2e passage on devrait résoudre x(t)=0 et trouver la deuxième plus petite valeur positive de t, si c'est le 3e passage la troisième plus petite valeur positive de t
C'est exactement ce que j'ai fait dans mon message du 18-06-25 à 14:44 :
Le premier passage en x=0 avec mouvement dans le sens positif correspond à k=0 soit t=T/8 ;
Le deuxième passage correspond à k=1 soit t=T/8+T ;
Le troisième passage correspond à k=2 soit t=T/8+2T
et ainsi de suite. Par définition de la période, la durée entre deux passages consécutifs à la même position et avec la même vitesse est T.
Cette animation, certes un peu "rustique", t'aidera peut-être à mieux comprendre le mouvement d'oscillation.
Annuler
connectez vous