Inscription / Connexion Nouveau Sujet
Oscillations Mécaniques
Bonjour, je rencontre des difficultés à comprendre un exercice. J'ai besoin d'aide. Voici l'énoncé.
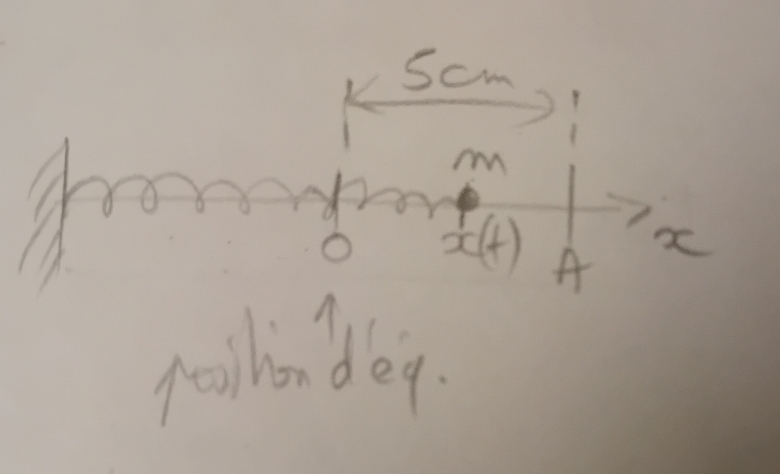
On considère un pendule élastique horizontal (voir croquis). Il est formé d'un ressort de raideur k=10N /m et d'un solide de masse m = 100g On écarte le solide de 5 cm de sa position d'équilibre puis on l'abandonne sans vitesse.
1) Ecrire l'équation différentielle du mouvement du solide. Ecrire l'équation horaire du mouvement. On choisira comme instant de date 0, l'instant où le solide passe par sa position d'équilibre déplaçant dans le sens positif.
2) Ecrire l'équation horaire de la vitesse.
Calculer les vitesses du solide:
au moment où il passe par sa position d'équilibre;
au moment où il passe par le point d'abscisse
- 2,5cm.
Je suis bloqué a la deuxième question
quand l énoncé dit ''On choisira comme instant de date 0, l'instant où le solide passe par sa position d'équilibre déplaçant dans le sens positif.''
c'est a dire qu'à t0 c est la position du solide quand on l'écarte et on le lâche ou bien plutôt c'est à la position d'équilibre ?
Bonjour,
Ça me paraît clair:
A l'instant t=0, le solide se trouve à la position d 'equilibre et sa vitesse est dans le sens positif (il faudrait poster la figure pour voir le repère utilisé)
Bonjour désolé de répondre aussi tard
Je vois maintenant.
Pour trouver l'équation du mouvement
Vu que la solution de l'équation admet une solution de la forme xmax cos(wt+fi)
A t=0, x=x(équilibre) x(eq)=xmax cos(fi)
x(eq)=xmax cos(fi)
J ai pensé à déterminer le x(équilibre) sauf que le ressort est horizontale et donc je trouve T=0 donc cela signifierait que x(eq)=0 ??
Avant de parler d'équation diff. ou d'équation du mouvement, il faudrait déjà preciser:
Le systeme: ici c'est le solide
le référentiel d'etude: .....
et ensuite le repère utilisé!
Car tant que x n'est pas défini on va avoir du mal à faire de la mécanique....
La figure n'a pas l air tres précise, y a-t-il un axe orienté indiqué sur la droite au moins? ou un repèrage décrit dans l'énoncé?
Dans l'énoncé on nous a dit quand on a écarté le ressort cela s'est fait le sens positif donc je suppose que l'axe de x sera orienté vers la droite
1) équation différentielle
Système solide
Référenciel terrestre supposé galiléen
Bilan des forces : Poids, Tension du ressort et réaction
Tci : T(vect)+P(vect)+R(vect)=ma(vect)
Suivant xx':
-T=m(d²x/dt²)  (k/m)x+(d²x/dt²)=0
(k/m)x+(d²x/dt²)=0
C'est bon?
C'est ça mais il faut bien préciser auparavant le repère (O,x) utilisé et donc definir la coordonnee x, voir figure ci-dessous , sinon ça ne veut rien dire.
D'accord
Ensuite pour la question 2
La solution de l'équation différentielle est de la forme x=xmax cos(wt+fi)
A t=0, x=x(eq)  x(eq)=xmax cos(fi)
x(eq)=xmax cos(fi)
Pour déterminer x equ j'ai pensé à utiliser la condition d'équilibre mais j'ai l'impression que ça mène à rien
definir la coordonnee x, voir figure ci-dessous , sinon ça ne veut rien dire.

Le x c'est l'allongement du ressort à l'équilibre dans mon équation différentielle
[
Le x c'est l'allongement du ressort à l'équilibre dans mon équation différentielle
Attention: dans le repère (O,x) choisi plus haut, O est la position d'équilibre du solide ( ici à l'equilibre, l'allongement du ressort = ..... ) et x est juste l'allongement du ressort.
L'allongement à l'équilibre est .... pour un ressort horizontal.
Et donc ici avec notre repère, xeq vaut ..... par définition de O.
2) équation horaire de la vitesse
En dérivant je trouve:
V(t)=-0,5sin(10t+(pi/2))
Vitesse du solide
Qd il passe par sa position d'équilibre :
V(t=0)=-0,5m/s
Qd il passe par x=-2,5cm
A x=2,5.10-² m, on a : -2,5.10-²=5.10-² cos(10t+(pi/2))
Cos(10t+(pi/2))=-1/2
Donc t=pi/60 ou t=-7pi/60 ( impossible)
V(t=pi/60)= -0,4 m/s
2)
Vitesse du solide
Qd il passe par sa position d'équilibre :
V(t=0)=-0,5m/s
n'y a-t-il pas un petit ennui avec cette valeur? Le solide se dirige vers les x positifs en t =0, non? Donc quel est le signe de v(0) ?
Oui c est vrai normalement j aurais du avoir 0.5 m/s
mais je vois pas du coup ou se trouve l erreur dans mes calculs...
Bonjour,
l'erreur est là:
D'accord je vois merci !
Avec fi=90 degré c ça ?
en fait ici, c'est -90°, je te laisse chercher pourquoi...
Ce sont les conditions initiales qui comptent pour déterminer les constantes d'integration.
Ici, à t=0, x=0 et on a une deuxième condition qui permet de trouver 
Je vois pas trop. Selon moi j'aurais dit c'est le fait qu'on nous dise que le solide se déplace dans le sens positif. Mais j'ai pas l'impression que ca va dans le sens pour avoir un fi négatif
Une facon de le voir:
À t=0 le solide se déplace dans le sens positif donc sa vitesse est ...
Donc tu calcules la vitesse en t=0 avec les deux valeurs de  possibles et tu tranches.
possibles et tu tranches.
Ahh d'accord je vois
Mais dans ce cas dans la question ou on devait donné l expression de l'équation horaire on devait pas trancher au niveau des fi
Si, il faut déterminer à la 1ere question, mais rien ne t'empêche de calculer la vitesse pour trouver
à la 1ere question, mais rien ne t'empêche de calculer la vitesse pour trouver  si tu ne vois pas une autre façon de faire
si tu ne vois pas une autre façon de faire
(ce qui va permettre de répondre a la 2nde question par la meme occasion, mais ca cest pas un pb)
Je vois donc qd on me dit le solide se déplace dans le sens des x positif il faudrait que le cherche la vitesse ( si j'ai pas d'autre façon de le faire ) et pas directement dire que c'est 90 prcq par exemple il se déplace dans les x positif ça n'a rien avoir si je compris bien
Et dans le cas où ya des frottements est ce que la solide bien que se déplaçant dans le sens des x positif peut avoir une vitesse négatif ?
Tu a trouvé une solution du type: x(t) = Xm cos(wt+ )
)
A t=0 , x(0) = 0 donc cos ( ) =0 (puisque Xm est non nul)
) =0 (puisque Xm est non nul)
Pour trouver  il faut donc une information supplementaire pour choisir entre + et -
il faut donc une information supplementaire pour choisir entre + et -  /2
/2
Ça ne se devine pas comme ça!
Ici on dit que le solide se déplace vers les x positifs a t=0 , donc sa vitesse est positive à t=0 (même en cas de frottement) et donc
x'(0) = -Xm w sin  >0 donc ....
>0 donc ....
C'est une façon de faire