Inscription / Connexion Nouveau Sujet
Oscillations mécaniques
Bonjour les amis 
J'aurais besoin d'aide pour cet exercice.
Merci de me guider pour ce nouveau chapitre 
L'énoncé :
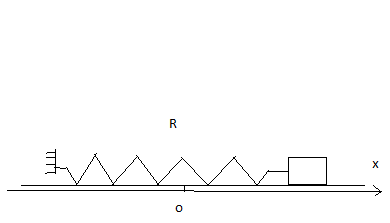
Un pendule élastique est constitué d'un ressort de raideur K =20N.m-1 et d'un solide de masse m qui peut osciller sur un banc à coussin d'air horizontal.
À l'instant t=0 ,le solide est écarté de sa position d'équilibre de x0= 2√2 cm et lâché avec une vitesse initiale v0 négative.
Partie 1
Dans un premier temps, on néglige les frottements du chariot sur le banc .
1) Faire l'inventaire des forces exercées sur le chariot et les représenter .
2) Établir l'équation différentielle du mouvement.
3) Vérifier que x(t)= Xm sin( 0t +
0t + ) est solution de cette équation différentielle avec
) est solution de cette équation différentielle avec  0 une constante que l'on exprimera en fonction des grandeurs physiques du système.
0 une constante que l'on exprimera en fonction des grandeurs physiques du système.
4) Établir une relation entre x, v , Xm et  0
0
5) En quel point la vitesse du mobile est maximale ?
Partie 2
Grâce à des capteurs appropriés ,on enregistre l'évolution temporelle de l'élongation x du centre d'inertie du chariot. On trace la courbe de la variation de l'énergie potentielle élastique Ep du système {chariot, ressort} en fonction du temps.
1) Montrer que Ep s'écrit sous la forme :
2) En exploitant le graphe ,déterminer la période propre des oscillations T ,l'amplitude Xm et la masse m du chariot.
3) Déterminer la phase initiale et l'expression de l'élongation x(t).
4) Déterminer v0
5) Montrer que l'énergie mécanique du pendule élastique est constante.
Bonsoir
Qu'as-tu été capable de faire pour l'instant ?
Où es-tu bloqué ?
Tu dois sûrement savoir qu'un ressort considéré ici comme idéal exerce une force de rappel sur le chariot colinéaire à son axe, de vecteur :
où est un vecteur unitaire horizontal colinéaire à l'axe du ressort.
L'origine des abscisses est la position d'équilibre du centre d'inertie du chariot.
La relation est ambigüe. Dans ce problème, de nombreux vecteurs horizontaux changent périodiquement de sens : vitesse accélération, tension du ressort... Dans ces conditions, il est habituel de noter par une simple lettre : a, v, T la composante non nulle de ce vecteur suivant
. Si le vecteur
est orienté vers la droite (sens de
) : T>0, s'il est orienté vers la gauche : T<0. Avec cette convention d'écriture, la relation vectorielle fournie dans mon message précédent conduit à :
T=-k.x
Puisque le poids du chariot est compensé par la réaction du sol horizontal, la relation fondamentale de la dynamique conduit à :
Soit :
En dérivant successivement deux fois l'expression fournie de x(t) , tu as montré que cette expression est bien solution de l'équation différentielle sous réserve que :
Conventionnellement, on retient la solution positive :
De même, on choisit conventionnellement Xm>0 ; les problèmes de signe se règle en ajustant la valeur de  mais cette détermination n'est pas demandée pour l'instant.
mais cette détermination n'est pas demandée pour l'instant.
Question 4 : je me demande s'il n'y a pas une faute de frappe dans l'énoncé tel que tu l'as recopié. Je pense qu'à cet endroit du problème, on demande juste d'exprimer v en dérivant x par rapport au temps. Une autre expression de v est possible en faisant intervenir la conservation de l'énergie mécanique mais cela est demandé plus tard dans le problème.
La question 5 ne devrait pas te poser de difficulté.
Pour le début de la partie 2, il faut connaître ses formules de trigonométrie :
On transforme un cosinus en sinus par un décalage astucieux de .
Je te laisse réfléchir à tout cela et proposer une solution...
Puisque l'altitude du centre de gravité du chariot est constante, l'énergie potentielle de pesanteur est une constante que l'on peut choisir arbitrairement nulle. Reste donc l'énergie potentielle élastique du ressort dont l'expression générale est ici :
En remplaçant x par l'expression fournie par l'énoncé et en tenant compte de mes remarques précédentes sur la trigonométrie, tu devrais t'en sortir... Je te laisse réfléchir.
Une remarque : le sinus fait intervenir (2 ) et non pas (2
) et non pas (2 .x) : étourderie j'imagine...
.x) : étourderie j'imagine...
D'accord avec ta première égalité :
La suite est fausse :
c'est comme si tu écrivais : alors qu'en réalité, comme je l'ai écrit plus haut :
mais l'application de cette relation te ramènerait à l'expression de départ. Pour obtenir celle de l'énoncé, il faut remarquer :
Les décalages de d'un angle transforme un sinus en cosinus ou inversement avec dans certains cas un changement de signe. Pour s'y retrouver simplement sans erreur, il faut tracer rapidement à main levée un cercle trigonométrique et y placer l'angle (b) et l'angle
.
Tu n'as pas bien compris ce que j'ai écrit sur l'énergie potentielle de pesanteur : On écrit souvent : Epp=m.g.z où z est l'altitude mais ici z = Constante . On peut donc choisir cette constante nulle : Epp=0
D'où l'expression de l'énergie potentielle totale fournie par l'énoncé et que tu as retrouvée.
Pour la suite, il faut exploiter un graphe que tu ne fournis pas. Je peux t'indiquer la méthode générale mais je ne pourrais pas vérifier les résultats sans ce graphe.
Il faut :
1° Mesurer graphiquement les valeurs de Xm et T ;
2° de la valeur de T, déduire la pulsation propre :
3° Connaissant la valeur de k, calculer la valeur de la masse m sachant, comme déjà démontré :
4° déterminer la valeur de  connaissant la valeur initiale de x et sachant que la vitesse initiale est négative : je t'ai expliqué la méthode dans l'autre post...
connaissant la valeur initiale de x et sachant que la vitesse initiale est négative : je t'ai expliqué la méthode dans l'autre post...
Oui
Pour 3.
À t=0 , x0= 2√2
2√2= Xmsin(wt+phi) ==>
sin phi= 2√2/Xm or j'ai trouvé Xm= 8 carreax d'après mon graphe
v0= 0
Cos (phi)= 0
C'est juste ?
Remarque préliminaire : mesurer 2 2cm n'a aucun sens physique ! Suivant le soin apporté, on peut ajuster x(0) à 2,8cm, avec beaucoup de soin, peut-être à 2,83cm mais certainement pas à 2
2cm n'a aucun sens physique ! Suivant le soin apporté, on peut ajuster x(0) à 2,8cm, avec beaucoup de soin, peut-être à 2,83cm mais certainement pas à 2 2cm !
2cm !
Tu obtiens :
2,83=Xm.sin( ) si Xm est mesuré en cm et :
) si Xm est mesuré en cm et :
v(0)= o.Xm.cos(
o.Xm.cos( )<0
)<0
Ayant mesuré graphiquement Xm, tu es en mesure d'obtenir  !
!
Essaie tout de même de scanner le graphe et de le poster sur le forum au format jpeg ou png ou gif... Une fois enregistré l'image sur ton ordinateur à un de ces trois formats, il suffit de cliquer sur l'icône "Img" et de suivre les instructions.
N'ayant pas le graphe, je peux toujours essayer de deviner... Les 8 carreaux dont tu parles ne représenteraient pas par hasard la différence entre la valeur maximale de x(t) et la valeur minimale de x(t) ? Pour peu alors qu'un carreau corresponde à 1cm, on obtiendrait : Xm= 4cm, soit, si  est exprimé en radians :
est exprimé en radians :
Je te laisse lever l'indétermination en raisonnant sur le signe du cosinus.
Sous toutes réserves en absence du graphe...
Pardon je vais attendre demain donc pour terminer les exos sinon j'écrirai des bêtises car je suis très fatigué 
Merci à demain ,bonne soirée 
Bonjour vanoise
v0<0 ==>
cos <0 =>
<0 =>
 = -π/4
= -π/4
x= 4cos (12πt -π/4)
C'est juste?
désolé, ce n'est pas à ma disposition un scanneur !
Mais on peut continuer ...je comprendrai
D'accord avec ta valeur de  en précisant bien qu'il s'agit d'une mesure en radians.
en précisant bien qu'il s'agit d'une mesure en radians.
Ayant posé  o
o 12
12 rad/s; j'imagine que tu as trouvé graphiquement une période d'environ un sixième de seconde.
rad/s; j'imagine que tu as trouvé graphiquement une période d'environ un sixième de seconde.
D'un exercice à l'autre, tu dois raisonner à partir des sinus ou des cosinus... Ici il s'agit des sinus :
si x(t) est mesuré en cm, on obtient :
Par dérivation, si v est mesurée en cm/s :
soit à t = 0 :
Presque !
Tu as oublié le carré de . Ensuite, en remplaçant
. Ensuite, en remplaçant  2 par sa valeur en fonction de k et m et en remarquant que la somme sin2+cos2 vaut....
2 par sa valeur en fonction de k et m et en remarquant que la somme sin2+cos2 vaut....
N'oublie pas que, derrière les calculs, il y a des lois physiques. Ici, dans la mesure où les frottement sont négligés, la théorie doit conduire à la conservation de l'énergie mécanique, c'est à dire à une énergie mécanique dont l'expression ne fait pas intervenir le temps...
Attention aussi à la rigueur des notations : tu notes la pulsation propre parfois  o comme demandé par l'énoncé, parfois
o comme demandé par l'énoncé, parfois  comme demandé dans d'autres exercices...
comme demandé dans d'autres exercices...
***Bonjour***
la question 4 : etablire une relation entre x ,v ,Xm et w0 ?
svp
Je n'ai pas vraiment compris comment répondre à cette question
La conservation de l'énergie mécanique conduit à :
En divisant tous les terme par la masse m, compte tenu de la définition de la pulsation...


