Inscription / Connexion Nouveau Sujet
Oscillations électriques libres 1
Bonjour, aidez-moi svp.
Problème : Un condensateur de capacité C chargé sous une tension constante U0 est déchargé à partir de la date 0 dans une bobine de résistance R et d'inductance L.
1) Montrer que l'équation différentielle qui régit la charge q du condensateur peut se mettre sous la forme :
Donner l'expression du degré d'amortissement .
2) Lorsque est inférieur à une certaine valeur
, on démontre que la solution de l'équation différentielle peut se mettre sous la forme
.
Montrer que l'on a .
3) Donner l'allure de la courbe q = f(t).
4) Donner l'expression du temps t1 au bout duquel l'amplitude de la charge devient-elle égale au 1/100 de sa valeur initiale.
Bonjour
Il s'agit d'obtenir une équation différentielle analogue à celle que tu viens d'obtenir en mécanique. La loi d'addition des tensions permet d'aboutir. Faire un schéma soigné en orientant correctement les dipôles.
D'accord et voici mon schéma 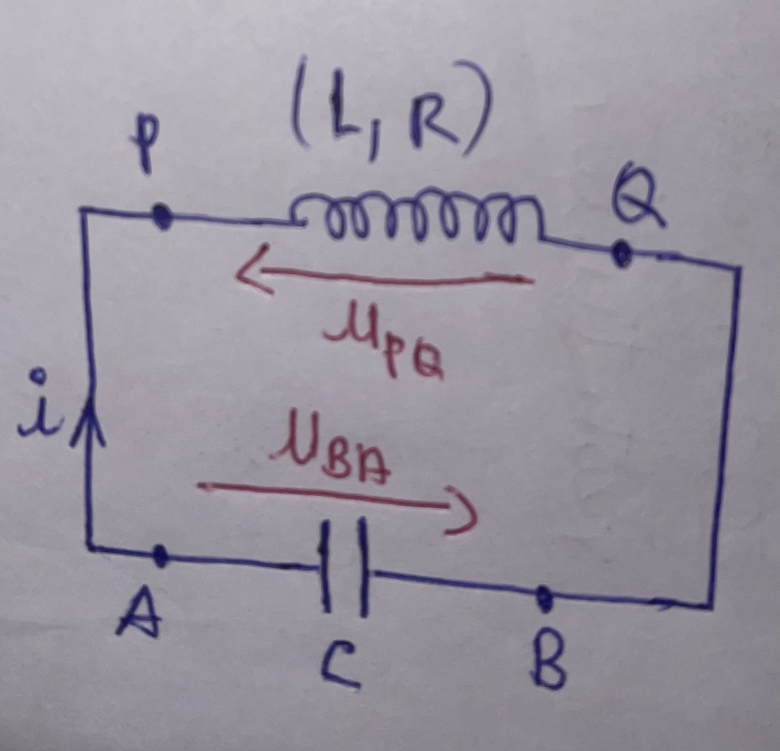
Question 1 : Équation différentielle du mouvement
• aux bornes de la bobine : Ub = L(di/dt) + Ri
Or i = dq/dt  di/dt = d2q/dt2 = q''
di/dt = d2q/dt2 = q''
Alors Ub = Lq'' + Rq'
• aux bornes du condensateur : Uc = q/c
La loi des mailles donne, après simplification :
En posant 2 = R/L
= R/L 
 = R/(2L)
= R/(2L)
et
Ainsi :
Expression du degré d'amortissement
du degré d'amortissement
En remplacement et la pulsation propre par leurs expressions, on trouve ceci :
et la pulsation propre par leurs expressions, on trouve ceci :
C'est ça ?
Question 2 : Montrons que l'on a
Je pense que la méthode consiste à dériver q(t) deux fois de suite et à remplacer dans l'équation différentielle.
Ensuite, petit arrangement de l'équation permet d'aboutir au résultat demandé. C'est ça ?
Bonjour,
Oui, c'est ça, mais je te conseille de mettre Q0 et e- t en facteur dans q, q' et q" puis dans l'équation finale. Comme ces deux termes ne sont pas nuls, tu peux les supprimer dans l'équation différentielle. Il ne reste plus qu'à regrouper les termes en sinus et cosinus et d'annuler leurs coefficients.
t en facteur dans q, q' et q" puis dans l'équation finale. Comme ces deux termes ne sont pas nuls, tu peux les supprimer dans l'équation différentielle. Il ne reste plus qu'à regrouper les termes en sinus et cosinus et d'annuler leurs coefficients.
Tu verras d'ailleurs qu'il ne reste que le terme en cosinus.
C'est ça ?
L'équation différentielle fait intervenir la dérivée première et la dérivée seconde de q par rapport à t. En substituant comme tu le suggères, tu vas obtenir quelque chose de la forme :
où A et B dépendent des différentes constantes. Comme l'équation précédente doit être vérifiée quel que soit t, il faut :
A= 0 et B=0.
Le résultat attendu sort facilement !
Je détaille ici mon travail.
•
•
•
Maintenant il suffit de remplacer dans l'équation différentielle pour aboutir à la relation demandée.
Cela est sans conséquence pour les deux premières questions mais il est possible que ton énoncé ne soit pas tout à fait cohérent, ce qui pose problème pour la question 3. Ton énoncé n'est pas précis à cet égard mais il est très probable que le condensateur, une fois chargé à l'aide d'un générateur de tension continue annexe, est relié à la date t=0 à la bobine (L,R). Celle-ci n'est parcourue par aucun courant avant sa connexion au condensateur. Or, tu sais que la présence d'une bobine dans une branche, impose la continuité de l'intensité du courant à travers celle-ci (voir autre exercice). La continuité de i à travers la bobine en t=0, impose donc une intensité nulle en t=0.
En t=0 :
Reprends ton calcul du 10-06-25 à 03:31 : il ne conduit pas à ce résultat. Conclusion : l'expression de q(t) fournie par l'énoncé ne convient pas. Il faut poser :
Alors :
Il est ainsi possible d'obtenir en t=0 si :
.
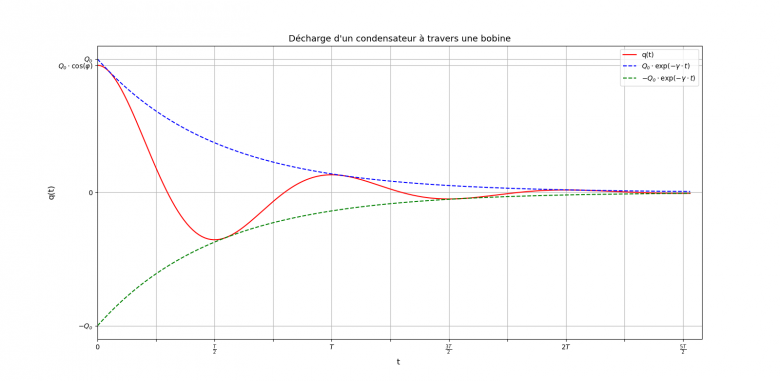
Ajouter ce déphasage ne modifie pas les résultats des deux premières questions mais modifie légèrement l'allure de la courbe q=f(t). En particulier, cette courbe doit présenter une tangente horizontale en t=0 (voir cours de math).
Sachant qu'un cosinus varie entre -1 et 1, la courbe q=f(t) doit être comprise entre les exponentielles d'équations et
.
Comme dans l'autre exercice, on peut définir une constante de temps : . Les deux exponentielles se confondent pratiquement avec l'axe horizontal q=0 au bout d'une durée d'environ 5
 .
.
N'ayant pas de valeurs numériques, j'ai choisi 5 voisin de 5T/2 mais cela est purement arbitraire de ma part.
voisin de 5T/2 mais cela est purement arbitraire de ma part.
Au niveau terminale, on se limite à l'étude de l'allure de la courbe. N'hésite pas tout de même à poser des questions si tu le juges utile.
Bonjour vanoise,
D'accord avec vous pour la rédaction de l'énoncé, qui m'avait aussi interpellé. Je pense que l'auteur a voulu éviter à l'élève d'avoir à calculer le déphasage donc de faciliter le tracé demandé. Par contre, il aurait alors fallu préciser que l'origine des temps est choisie à l'instant où q est de la forme Q0e- tcos(
tcos( t).
t).
Bien sûr, ceci entraîne que i(t) n'est pas nul à l'instant t=0.
Bonjour fph67
Ce genre d'énoncé se rencontre souvent lorsque l'on pose au niveau "n" un exercice de niveau "n+1" ... Le concepteur, en voulant rendre l'exercice plus facile, se permet quelques entorses à la physique ou quelques non-dits.
Comme hdiallo est quelqu'un de motivé qui cherche à approfondir, je me suis permis de présenter les choses comme cela se fait habituellement au niveau (bac+1).
Merci vanoise et merci fph67.
J'ai pris tout mon temps à analyser cette remarque et j'ai bien compris.
• En effet, partant de l'expression q(t) fournie par l'énoncé, on a :
- à l'instant t quelconque :
- à l'instant initial (t = 0) :
Conséquence : i est different de zéro
• Or, la continuité de i à travers la bobine en t=0, impose donc une intensité nulle en t=0.
Du coup, la bonne expression de q(t) aurait pu être ceci
Ainsi :
Dans ce cas, à l'instant initial (t = 0) :
Si et seulement si .
J'ai bien compris aussi la courbe. Je me rappelle d'une autre courbe identique à celle-ci, en oscillation mécanique, où on avait même demandé de calculer le décrément logarithmique.
À présent la dernière question…
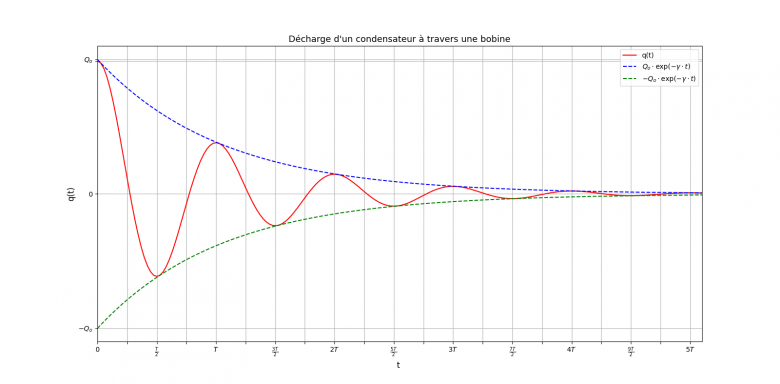
Je crois que tu as bien compris. L'essentiel à retenir étant bien sûr la continuité de l'intensité imposée par la bobine. Pour simplifier le tracé de la courbe q=f(t), on peut choisir un amortissement plus faible. Voici par exemple ce que l'on obtient en divisant  par 2 sans modifier
par 2 sans modifier  o. Le déphasage
o. Le déphasage  est beaucoup plus faible (8,6° au lieu de 17,5° pour mon exemple) de sorte que la valeur initiale Qo.cos(
est beaucoup plus faible (8,6° au lieu de 17,5° pour mon exemple) de sorte que la valeur initiale Qo.cos( )
) Qo.
Qo.
De même, l'expression de l'intensité peut se simplifier :
Les extrémums de la courbe q=f(t) correspondent pratiquement aux dates où la courbe admet un point commun avec l'une ou l'autre des deux exponentielles tracées en pointillés.
PS : tu as raison : l'étude est très analogue à celle d'un oscillateur mécanique avec frottement proportionnel à la vitesse.
Merci.
Question 4)
Q0.e(- t1) = Q0/100
t1) = Q0/100
Donc  t1 = 10ln10
t1 = 10ln10  t1 = (10ln10)/
t1 = (10ln10)/
Avec  = R/(2L)
= R/(2L)
Mais vanoise, aucune valeur n'est donnée, donc impossible de faire l'application numérique
D'accord ! En introduisant, comme cela a déjà été fait dans l'exercice précédent, la constante de temps  =1/
=1/ , cela donne :
, cela donne :
t1=2 .ln(10)
.ln(10) 4,6
4,6
Cela est heureusement cohérent avec la date t2=5 déjà évoquée qui correspond sensiblement à 0,67.10-2.Qo.
déjà évoquée qui correspond sensiblement à 0,67.10-2.Qo.
PS : le concepteur de l'énoncé "récidive" dans cette question 4) en considérant Qo comme la charge initiale mais bon : en considérant la décharge très peu amortie : Qo.cos( )
) Qo comme déjà expliqué !
Qo comme déjà expliqué !


