Inscription / Connexion Nouveau Sujet
Oscillations électriques forcées 2
Bonjour, aidez-moi svp.
Problème : On considère le circuit ci-dessous :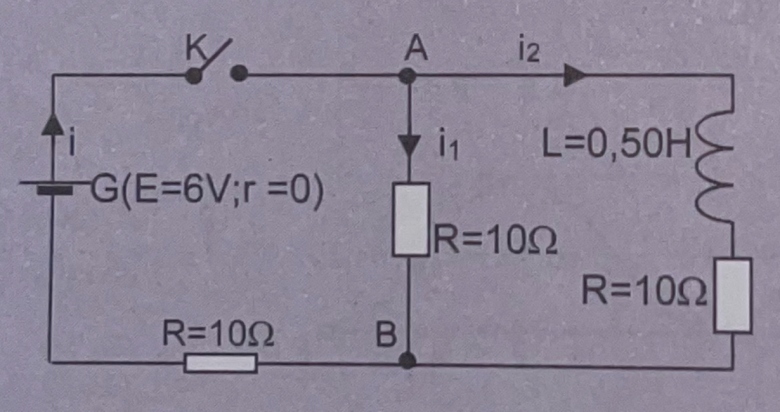
1) Écrire la loi d'Ohm pour les différentes branches. En déduire l'équation différentielle à laquelle obéit l'intensité i du courant principal.
Quel est le régime du courant dans chaque branche ?
2) Sachant que l'interrupteur K est fermé à la date choisie comme date 0 et que l'intensité du courant principal est de la forme .
Calculer A, B et  .
.
Bonjour
La méthode consiste à appliquer la loi des nœuds en écrivant l'expression de la tension entre A et B de trois façons différentes.
D'accord.
Question 1
Au nœud A : i = i1 + i2
• branche contenant le générateur :
UAB = Ri - E
• branche contenant la branche du milieu :
UAB = Ri2
• branche contenant le bobine :
UAB = ???? Aidez moi ici
Bonjour,
Attention : UAB = VA - VB
Aucune de tes relations de tension n'est correcte, erreur de signe ou erreur sur le courant
Il faut corriger en :
UAB = E - Ri
UAB = R.i1
Pour la 3ème branche, il faut te rappeler que UL = L.di2/dt
Tu dois maintenant pouvoir écrire UAB par la 3ème branche ...
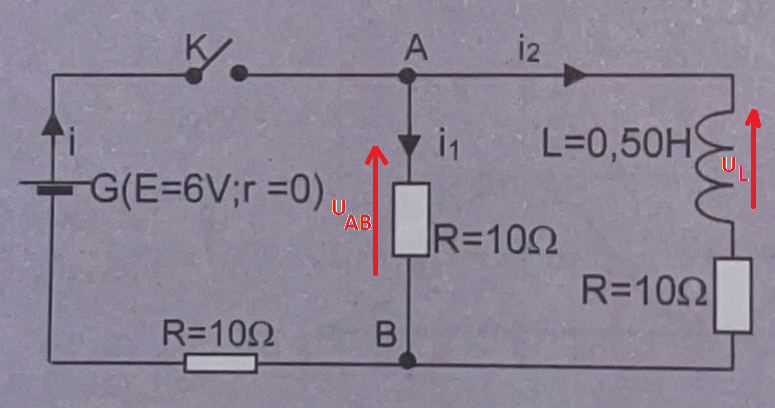
Bonsoir hdiallo
Pour éviter les erreurs de signes, tu as toujours intérêt à orienter tous les dipôles du circuit. Cela commence par préciser pour chaque branche, à l'aide d'une flèche sur le fil, le sens conventionnel positif du courant : cela est déjà fait ici.
Ensuite, il faut indiquer à côté de chaque dipôle, la flèche de définition de la tension aux bornes de ce dipôle. Voir si nécessaire le document ci-joint rappelant les conventions. Bien voir alors si le dipôle est orienté selon la convention récepteur ou selon la convention générateur : cela influence les signes et sans ce travail préliminaire, les fautes de signes sont fréquentes. Par exemple, pour un conducteur ohmique en convention récepteur, la loi d'Ohm s'écrit U = R.i alors qu'en convention générateur, elle s'écrit : U=-R.i !
Voir document ci-dessous ; n'hésite pas à poser des questions complémentaires si tu le juges utile !
![]()
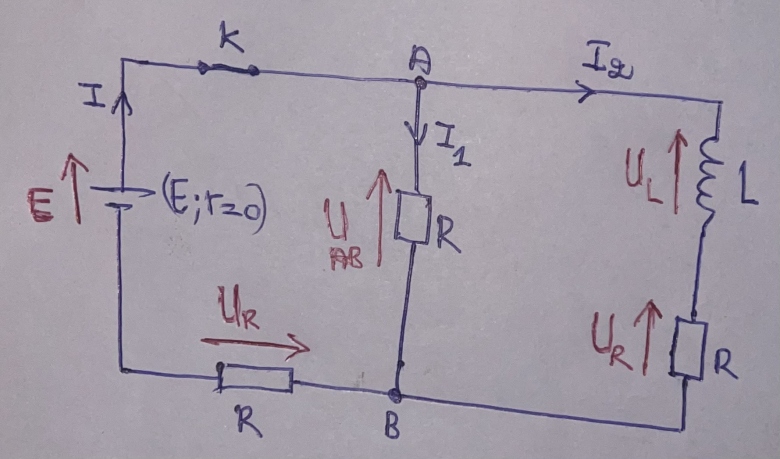
Voici le schéma avec orientation du dipôle, en rouge la flèche de la tension.
• branche contenant le générateur :
UAB = E + RI
• branche du milieu : UAB = RI1
• branche contenant la bobine :
UAB = L(dI2/dt) + RI2
La loi des noeuds permet d'écrire : I = I1 + I2
Tu as bien orienté les dipôles mais ensuite, la loi d'addition des tensions correspond à la loi d'addition des vecteurs...
Si on récapitule, on obtiens, comme expliqué dans mon premier message, trois relations indépendantes :
Tension commune aux branches gauche et droite :
Tension commune aux branche gauche et centrale :
Loi des noeuds :
Méthode possible pour obtenir l'équation différentielle : partir de l'équation (1) et exprimer i2 en fonction de i puis di2/dt en fonction de di/dt en utilisant les relations (2) et (3).
Éliminer i1 entre les relation (2) et (3) ; cela donne l'expression de i2 en fonction de i, R et L. Dériver par rapport au temps donne la relation entre di2/dt et di/dt.
On reporte dans (1) et le tour est joué !
Merci.
• De la relation (2) :
• De la relation (3) : i2 = i - i1
En remplaçant i1 par son expression on trouve ceci
Donc
Dans (1) :
Soit
D'où l'équation différentielle demandée :
Merci
On demande à présent de préciser le régime du courant dans chaque branche.
Tout dépend du générateur, à mon avis.
S'il débite un courant continu, alors le régime est continu, sinon il est alternatif.
L'énoncé précise clairement qu'il s'agit d'un générateur de tension continu.
La solution de l'équation différentielle précédente est de la forme :
.
Cette expression dépend du temps mais le terme variable décroît exponentiellement en fonction du temps pour devenir d'influence négligeable au bout d'une durée d'environ 5 . On considère en effet en physique : exp(-x)
. On considère en effet en physique : exp(-x) 0 pour x>5. Tu veux vérifier avec ta calculatrice. Le courant traversant le générateur est donc un courant transitoire de durée voisine de 5
0 pour x>5. Tu veux vérifier avec ta calculatrice. Le courant traversant le générateur est donc un courant transitoire de durée voisine de 5 suivi d'un courant continu. On parle de régime transitoire. En utilisant les relations de ton message du 09-06-25 à 15:37, tu peux montrer qu'il en est de même pour les deux autres courants...
suivi d'un courant continu. On parle de régime transitoire. En utilisant les relations de ton message du 09-06-25 à 15:37, tu peux montrer qu'il en est de même pour les deux autres courants...
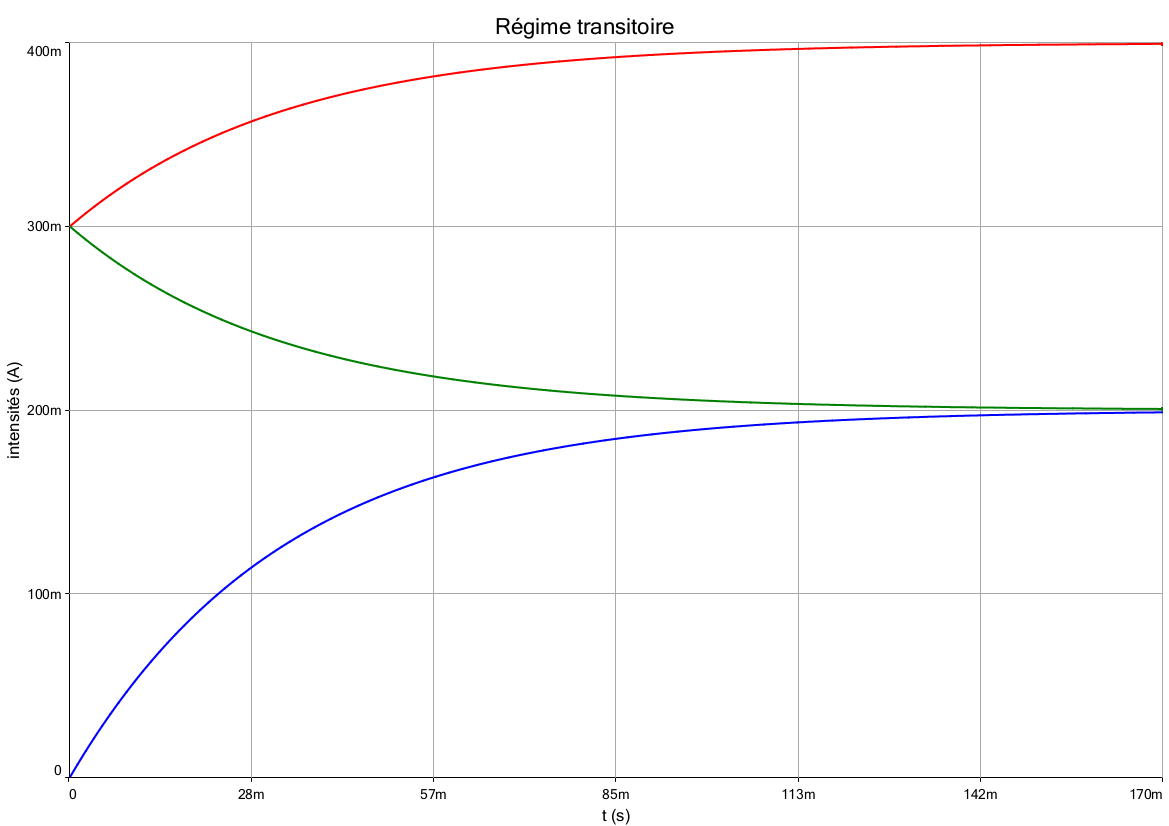
Pour illustrer cela et te permettre de t'auto-corriger pour les résultats suivants, voici une simulation représentant les variations en fonction de t des trois intensités. Je te laisse le soin d'identifier les trois courbes. (la lettre "m" signifie "milli" pour les graduations des axes).
L'énoncé précise clairement qu'il s'agit d'un générateur de tension continu.
Je ne vois pas ce passage dans l'énoncé
vanoise, la courbe du bleu représente i, celle du rouge représente i2 et la courbe en vert représente i1.
D'où proviennent les valeurs particulières 300 mA, 400 mA et 170 ms du graphique ?
Tu as sans doute vue en cours qu'une bobine impose la continuité de l'intensité dans sa branche au cours de temps. Les intensités étant nulles avant fermeture de l'interrupteur, i3=0 en t=0 à la fermeture de l'interrupteur. Cela permet déjà d'identifier la courbe bleue.
A t=0, tout se passe comme si la branche de droite n'existe pas. L'étude du reste du circuit impose donc à t=0 :
i=i2=E/2R.
Pour t>5 , le régime continu est atteint. La bobine se comporte alors comme un simple fil, la branche de droite est équivalente à une résistance R. Facile alors de trouver les valeurs asymptotiques des trois intensités...
, le régime continu est atteint. La bobine se comporte alors comme un simple fil, la branche de droite est équivalente à une résistance R. Facile alors de trouver les valeurs asymptotiques des trois intensités...
Tout cela permet d'identifier les trois courbes et de calculer les valeurs de A et de B.
Ensuite, comme dans l'autre exercice, exprime la dérivée di/dt et reporte dans l'équation différentielle. Cela va te permettre d'exprimer  en fonction de L et R.
en fonction de L et R.
Je ne vois pas ce passage dans l'énoncé
exact mais regarde bien le symbole du générateur sur le schéma fourni.
vanoise , je commence à perdre le fil.
Tu parles de i3 que je ne vois pas.
Ensuite, à t = 0, tous les courants sont nuls. Normalement, toutes les courbes devraient bouger à l'origine du repère. Mais je constate que 2 courbes (bleue et verte) bougent au point (0, 300mA).
La courbe en vert décroît et tend vers 200 mA tandis que la courbe en rouge croît et tend vers 400 mA. C'est ce que je ne comprends pas.
La courbe en bleu représente la variation variation du courant dans la bobine, si je comprends bien. C'est ça ?
La courbe en bleu représente la variation variation du courant dans la bobine, si je comprends bien. C'est ça ?
Oui ! Désolé pour mon étourderie sur les indices : c'est bien i2=0 et i=i1=E/2R=300mA en t=0.
Pour t tendant vers l'infini (en pratique t>5
 ), la bobine se comporte comme un fil. Tout se passe comme si la branche de gauche (E,R) alimente deux résistance R en parallèle, donc une résistance équivalente à R/2.
), la bobine se comporte comme un fil. Tout se passe comme si la branche de gauche (E,R) alimente deux résistance R en parallèle, donc une résistance équivalente à R/2.
Pour t>5
 : i=E/(1,5R)=400mA
: i=E/(1,5R)=400mA
quel est le symbole d'un générateur délivrant une tension sinusoïdale ?
Un cercle avec à l'intérieur une période de sinusoïde.
Petit complément : compte tenu du circuit équivalent pour t>5 déjà décrit :
déjà décrit :
i1=i2=i/2=200mA pour t tendant vers l'infini.
Oui ! 
Il te reste à déterminer les valeurs de A, B et  . La valeur de
. La valeur de  permet de comprendre pourquoi l'étude est effectuée entre zéro et 170ms.
permet de comprendre pourquoi l'étude est effectuée entre zéro et 170ms.
Je me suis absenté un peu longtemps, je suis désolé. C'est la fin de l'année scolaire, donc la période des évaluations finales.
Maintenant, vive les vacances !
Vive ilephysique.net !
Question 2 : calcul des constantes A, B et 
, alors
Or l'équation différentielle est
Par substitution :
Alors
Par comparaison du 1er et 2nd membre, on a :
AN :  = 0,03 s
= 0,03 s
C'est ça ?
Oui mais ne pas se contenter d'un seul chiffre significatif. Je dirais plutôt : 
 33,3ms.
33,3ms.
Ainsi : 5
 167ms. Voila pourquoi la simulation a été faite sur une durée de 170ms.
167ms. Voila pourquoi la simulation a été faite sur une durée de 170ms.
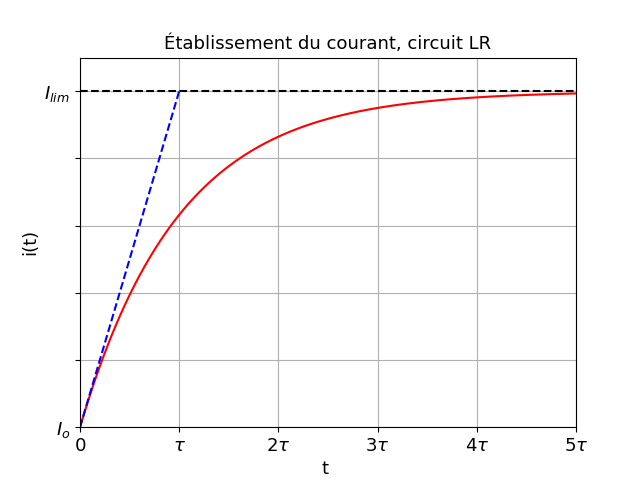
La question n'est pas posée ici mais très souvent, l'énoncé demande de tracer "l'allure" de la courbe. Je rappelle ici la méthode générale,, commune aux grandeurs solutions d'une équation différentielle du premier ordre car la courbe précise a été déjà tracée. Pour plus de généralité, le note Io la valeur initiale et Ilim la valeur asymptotique.
Deux points essentiels :
1° : comme déjà expliqué, la courbe se confond pratiquement avec l'asymptote horizontale pour t>5 .
.
2° : la tangente à la courbe en t=0 rencontre l'asymptote à la date t1= .
.
Ces deux remarques suffisent à tracer "l'allure" de la courbe. Éventuellement, on obtient un peu plus de précision en ajoutant la valeur de i(t1) en remarquant :
i( )=I0+(Ilim-I0)(1-e-1)
)=I0+(Ilim-I0)(1-e-1) 0,632.(Ilim-I0).
0,632.(Ilim-I0).

 i2
i2

