Inscription / Connexion Nouveau Sujet
Oscillateurs mécaniques
Bonjour, chers professeurs.
J'espère que vous allez bien.
Je suis tombé sur un exercice de physique très intéressant et assez énigmatique. J'ai plusieurs hypothèses sur sa solution et je voudrais savoir si je suis sur la bonne voie mais je voudrais aussi votre assistance et votre aide.
Exercice :
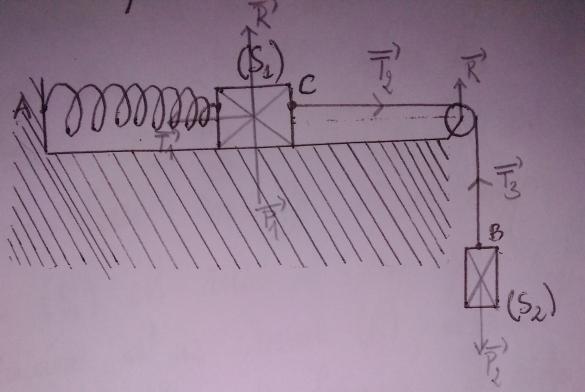
Un solide (S1) de masse M1=400g posé sur une table horizontale, est attaché en C à un fil inextensible, de masse négligeable. Ce fil passe sur la gorge d'une poulie mobile sans frottement autour d'un axe horizontal (∆) et supporte à son extrémité libre B, un solide (S2) de masse m2=m1/10. La poulie est un disque homogène de masse m=M1/20 et de rayon r=1cm. Le solide (S1) est relié à un point fixe A par l'intermédiaire d'un ressort (R), à spires non jointives de masse négligeable, de longueur à vide lo=10cm (Voir la figure).
1-Le système étant en équilibre, la longueur du ressort l=12cm. Calculer la constante de raideur du ressort.
2-À partir de sa position d'équilibre, on déplace (S2) verticalement vers le bas, de la longueur a=1cm et on l'abandonne sans vitesse initiale que le fil reste toujours tendu.
Écrire l'équation horaire de ce mouvement en prenant, pour origine des espaces, la position d'équilibre de (S2) et pour origine des temps l'instant où on lâche (S2). Préciser le sens positif choisi pour l'axe.
Mes idées :
Pour résoudre la question 1, j'ai commencé par faire l'étude dynamique : le système est le solide (S1) de masse m1, le référentiel est terrestre supposé Galiléen lié à un repère orthonormé (o;i;j). Le bilan de forces: Le poids P1 du solide (S1), la tension T2 du fil, le poids P2 de (S2), la réaction R2 de la poulie, la tension T3 du fil, la réaction R1 de (S1), la tension T1 du ressort.
J'applique le TCI: j'ai la somme de toutes ces forces qui est égale au vecteur nul car le système est en équilibre. Quand je fais une projection sur l'axe des abscisses, j'obtiens : -T1+T2=0 ce qui conduit à -Kx+T2=0.
Après ça, je me suis arrêté. Je pense obtenir plus tard T2/x=K avec x=10 et devoir déterminer T2 en m'occupant de la poulie.
Voilà, avant d'aller plus loin, je voudrais votre avis sur mes idées et des explications plus approfondies au cas où il le faille.
Bonjour
Il est sans doute plus simple de raisonner sur la conservation de l'énergie mécanique de l'ensemble du dispositif en absence de frottement. Cela évite l'étude des tensions des fils...
Donc, je procède par la méthode énergétique, je trouve une expression de l'énergie mécanique, je la dérive d'après la loi de conservation de cette dernière et je devrais trouver la constante de raideur ?
J'en étais déjà à la seconde question...
La première question demande une étude statique, pas une étude dynamique. Il faut effectivement écrire successivement la condition d'équilibre de chacun des trois solides en faisant intervenir les tensions des fils. Cela va te conduire à l'expression de 
l=l-lo en fonction de k et de m2.g.
L'équilibre de S1 conduit à T1=k.l=T2
L'équilibre de la poulie conduit à T2=T3 (je te laisse faire la démonstration)
L'équilibre de S2 conduit à T3=m2.g
A toi de terminer.
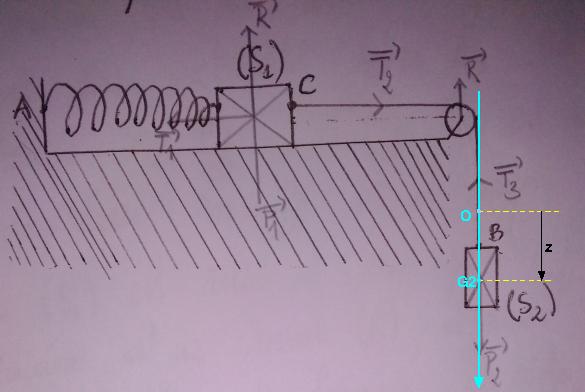
Pour la question 2 : tu peux choisir un axe vertical (Oz) orienté vers le bas dont l'origine O est la position d'équilibre du centre d'inertie de S2. Ainsi, au cours du mouvement d'oscillation, la cote du centre d'inertie G2 de S2 est z et pour le ressort :
(l-lo)=l+z
C'est là que le raisonnement sur l'énergie mécanique du système complet prend tout son intérêt. Tu écris l''expression de l'énergie mécanique Em. Comme celle-ci reste fixe :
(dEm/dt)=0 
t : cela conduit à l'équation différentielle vérifiée par z. Résoudre cette équation différentielle fournit l'équation horaire du mouvement : z=f(t).
J'ai donc établi les conditions d'équilibre de chaque sous système.
Pour le système (S1), j'ai appliqué le TCI et ça m'a donné -T1+T2=0, donc T1=T2=k∆l.
Pour le système de la poulie j'ai appliqué la RFDR impliquant les moments de T2, T3 et R mais le moment de R étant nul, il me reste les moments de T2 et T3. En projetant suivant le sens du mouvement j'obtiens dT2-dT3=0, d'où T2=T3.
Pour le système (S2), j'applique à nouveau le TCI et j'ai la somme du poids P2 et T3=0. Après la projection suivant l'axe (y'y), j'obtiens P-T3=0. Donc P=T3=m2.g.
Ensuite j'ai fait un système où j'ai pu obtenir la relation K=m2.g/∆l. En somme, je trouve K=2N.m.
Est-ce correct ?
J'ai un peu de mal à comprendre l'idée au niveau de la question 2. Devrais-je en quelques sortes retrouver l'équation différentielle d'un MRS comme pour les pendules élastiques verticaux ?
D'accord avec l'expression littérale de k. Il faut revoir l'application numérique.
Ensuite pour l'énergie mécanique :
1° : tu peux choisir comme état d'énergie potentielle de pesanteur nulle, l'état d'équilibre. Que vaut dans ces conditions l'énergie potentielle de pesanteur quand l'altitude de S2 diminue de "z" ?
2° : l'énergie potentielle élastique du ressort s'écrit : ½k(l-lo)2 ; à exprimer en fonction de k, z et l...
3° : l'énergie cinétique est une somme de trois termes puisque le système est formé de trois solides. Ces trois termes peuvent s'exprimer en fonction de (dz/dt) et des masses si on considère le fil inextensible, de masse négligeable, ne glissant pas sur la gorge de la poulie.
Oui, pour le calcul de la constante de raideur, je viens de me rendre compte que je n'ai pas utilisé g dans mon calcul.
Concernant la question deux, vous dites que l'énergie potentielle de pesenteur est nulle du fait de l'équilibre du système ? Ne serait-ce pas plutôt l'énergie potentielle élastique du fait de l'inextensibilité du fil ? Le "z" est-ce en fait le "a" de l'exercice qui est égal à 1cm ?
La formule ½k(l-lo) est en fonction de k et de ∆l. Comment la mettre en fonction de z ?
C'est un peu flou à ce niveau.
Concernant la question deux, vous dites que l'énergie potentielle de pesenteur est nulle du fait de l'équilibre du système ?
Le "z" est-ce en fait le "a" de l'exercice qui est égal à 1cm ?
Non : "z" est la coordonnée non nulle du centre d'inertie de S2 au cours du mouvement ; c'est une grandeur qui dépend de t. "a" est la valeur de z à la date t = 0.
L'énergie potentielle élastique du ressort s'écrit :
½k(l-lo)2 = ½k(
l+z)2
Tu vas constater plus tard, en posant : (dEm/dt)=0 que
l disparait du calcul compte tenu de la condition d'équilibre écrite précédemment.
Reste l'expression de l'énergie cinétique Ec mais je t'ai déjà fourni des indications à ce sujet....
Schéma annoté pour mieux faire comprendre le repérage de la position de l'oscillateur à une date "t" quelconque. La figure correspond à une situation telle que z>0 mais, puisqu'il y a oscillation, z est la moitié du temps positif, la moitié du temps négatif.
Je crois que j'ai saisi.
J'ai donc suivi vos conseils et j'abouti à l'équation différentielle de la forme z(point point)+(k/m)z=0.
Après que faire ?
Si le m de ton équation désigne la masse de la poulie, le résultat est faux. Quelle expression de l'énergie cinétique as-tu ?
Ensuite, en tenant compte des conditions initiales, il faut obtenir une solution de l'équation différentielle de la forme :
z =Zm. cos (
o.t+
) .
m désigne la masse de (S2).
Ec=½mx(point)2.
Comment passer de l'équation différentielle à l'équation horaire ? Pour ma part, je n'ai jamais eu à passer d'abord par l'équation différentielle avant d'arriver à l'équation horaire.
m désigne la masse de (S2).
Tu vas sans doute être amené un jour à passer des examens ou des concours... Il est indispensable de respecter les notations de l'énoncé et de rester cohérents sur les notations supplémentaires que l'on est amené à choisir. L'énoncé est clair : "m" désigne la masse de la poulie, celle de S2 est notée m2, celle de S1 : m1 (ou M1 ? Tu as utilisé les deux notations dans ta copie de l'énoncé)
Pour plus de clarté, j'ai complété ton schéma en ajoutant un axe vertical (Oz) puisque, en général, l'axe (Ox) est choisi pour caractérisé la position lors de déplacement horizontal. A priori j'ai perdu mon temps puisque tu utilises x et non z dans ton dernier message.
Tu n'as absolument pas tenu compte du point n° 3 de mon message du 26-06-20 à 18:23 : à cause du fil, il y a trois solide en mouvement : deux en translation (S1 et S2) et un en rotation autour d'un axe fixe : la poulie. L'énergie cinétique du système est la somme des trois énergies cinétiques des trois solides. Son expression doit faire intervenir m1,m2,m et
Au sujet de l'usage de x plutôt que z, c'est l'habitude qui m'a poussé à le faire.
La masse de S1 est m1, la correction automatique a parfois tendance à mettre le "m" en majuscule. Dans l'équation différentielle, en effet j'aurais dû mettre m2, c'est une erreur causée par une inadvertance.
J'avais oublié le point n°3. Je vais essayer de le prendre en compte.
L'équation du mouvement est de la forme z=zmsin(t+).
À t=0, zm=10-2m.
=π car sin=0 et cos<0. Ce qui montre que le sens positif pour moi est celui du poids P2 de (S2).
D'où, l'équation horaire de (S2) est: z=10-2sin(t+π).
Il faut traiter la situation initiale rigoureusement. Si tu cherches la solution générale sous la forme : ; la vitesse a pour expression générale :
.
Tu as un problème à deux inconnues : Zm et . Il te faut deux équations déduites des conditions initiales :
Pour t= 0 :
Je te laisse établir de façon rigoureuse les expressions de Zm et .
Reste en suspens le problème de la pulsation propre . On peut exprimer l'accélération :
z(t) est donc solution de l'équation différentielle :
Pour obtenir la valeur de la pulsation propre, il est donc indispensable de commencer par établir, à partir des lois de la mécanique, l'équation différentielle vérifiée par z(t) pour obtenir l'expression de la pulsation propre en fonction de k et des trois masses.
Est-ce Zm et
déterminés au préalable sont faux ?Quand on obtient un résultat littéral, il est prudent d'en vérifier le réalisme sur un cas particulier simple, par exemple le cas t=0.
Poser comme tu l'as fait :
Est-ce conforme l'énoncé ? Je t'ai indiqué la méthode à suivre pas à pas . Tu n'as toujours pas obtenu l'équation différentielle vérifiée par z(t)... Tu sembles bloqué par l'expression de l'énergie mécanique. Reprends mes messages précédents...
Annuler
connectez vous