Inscription / Connexion Nouveau Sujet
Optique géométrique
Bonjour, pourriez-vous m'aider pour un exercice? S'il vous plaît
Enoncé:
Un photocopieur permet de reproduire un document formant son image sur un tambour photosensible. On assimilera l'objectif du photocopieur à une lentille mince convergente et le tambour photosensible à un écran plan, orthogonal à l'axe optique de la lentille.
Questions:
a- L'image obtenue est-elle réelle ou virtuelle, droite ou renversée?
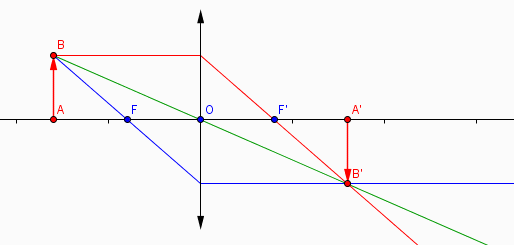
b- Sur un schéma sans soucis d'échelle, représenter l'objet AB et son image A'B'
c- En traçant un rayon de lumière particulier, montrer que le centre optique de la lentille est le milieu du segment AA'
d- Retrouver cette position à partir de la formule de grandissement
Je ne demande pas de me faire l'exercice, seulement de l'aide parce que j'ai déjà passer presque 1h sur cette exercice sans savoir comment faire. Je bloque totalement.
Merci a ceux qui voudront bien m'aider 
Bonjour,
As-tu commencé par apprendre ton cours ?
Dans quelles conditions peut-on obtenir une image sur un écran quand on dispose d'une lentille convergente ?
L'image est-elle dans ces conditions réelle ou virtuelle, droite ou renversée ?

Mon cours je l'ai appris, puis relu des dizaines de fois mais je n'ai pas réussi..
Mon professeur a dit que lorsque le l'objet se trouve entre le foyer objet et la lentille, l'image est virtuelle. Donc je suppose qu'il faut que l'objet soit situé avant le foyer objet. Je n'ai pas plus d'information que ça dans ma leçon (pour cette question)
Je n'y arrive pas, je comprends pas.
Oui, il faut que l'objet soit situé avant le foyer objet.
Même réponse : il faut que la distance de l'objet au centre optique de la lentille soit supérieure à la distance focale.
Il y a dans ton livre des schémas correspondant à ce cas.
L'image est-elle réelle ou virtuelle, droite ou renversée ?

L'image est réelle et renversée?
J'ai regardé un manuel que j'ai et ils disent que l'image est réelle et renversée si l'objet est situé entre - l'infini et F. Mais c'est vrai tout le temps?
Oui, c'est cela.
Quand l'objet est situé entre l'infini et le foyer objet, son image donnée par une lentille convergente est réelle (donc elle peut être recueillie sur un écran, ce qui est indispensable ici) et renversée.
La distance entre l'objet et la lentille n'est pas du tout quelconque car on veut que le grandissement soit égal à -1
Cela tu dois le voir en répondant aux questions b) et c)
As-tu fait le schéma ?

POur le schéma,je dois placer l'objet AB et et son image A'B' sans me soucier de l'échelle, je les mets a n'importe quelle distance de la lentille?
Oui, mais attention : AB et A'B' ont la même taille, sachant que A'B' est renversée par rapport à AB

J'ai fais le schéma, il a l'air d'être correct. Je ne peux pas le joindre a mon message, ça ne marche pas..
Ils parlent d'un rayon de lumière particulier mais lequel? Pour trouver l'image A'B' j'ai tracer les rayon lumineux qui passent par le centre optique et par le foyer image.
Merci! 
Quel rayon lumineux est ce que je dois utilisé pour répondre a la question c?
J'ai tracé les 3 seuls que je connais (il y en a que deux sur le schéma) mais je comprends pas comment je peux le montrer
Appelle O le centre optique de la lentille.
Considère par exemple les deux triangles rectangles ABO et A'B'O
Que peux-tu en dire ?
Ou encore souviens-toi du théorème de Thalès (configuration "papillon").

Je sais pas si ça marche mais ils sont tous deux symétriques par rapport a O.
Pour Thalès je vois comment l'appliquer mais pas trop comment expliquer...
Les triangles rectangles sont égaux :
. rectangles en A et A' (sur ma figure)
. opposés par le sommet, les angles et
ont même mesure
. les côtés AB et A'B' ont même longueur
Donc les triangles sont égaux et en particulier OA = OA'
________
Avec Thalès tu vas retrouver directement la réponse à la dernière question.
Que vaut le grandissement ? (j'ai déjà donné la réponse...)
Quelle relation te permet de trouver le grandissement ? Application...
Attention : je te conseille vivement d'utiliser les mesures algébriques et pas les simples longueurs de segments.

Pour répondre a la question d):
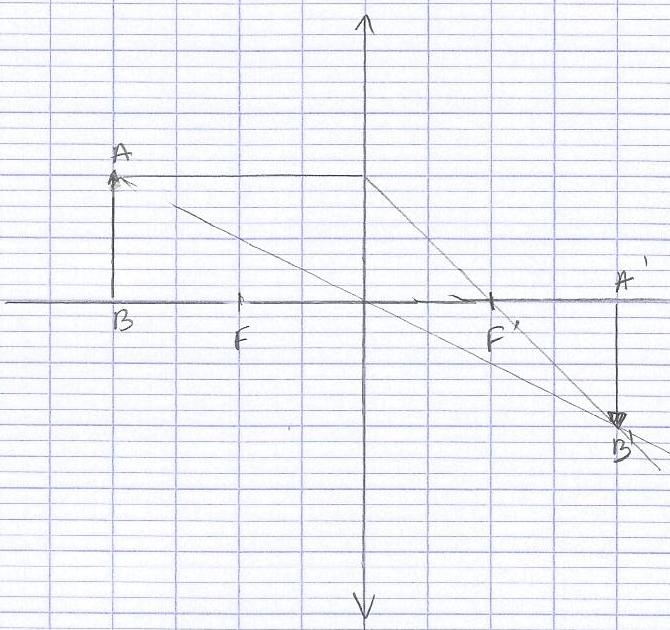
J'ai retracer le schéma sur du papier milimétré et j'ai utilisé les longueurs pour pouvoir trouver la grandissement

Pour répondre à cette question il faut
. d'abord bien lire l'énoncé
. connaître son cours
Bien lire l'énoncé : "on veut reproduire le document" ; on ne veut ni l'agrandir ni le réduire
Connaître son cours : l'image donnée est renversée (comme tu as pu le retrouver dans les schémas que nous avons faits)
Donc : que vaut le grandissement dans une photocopieuse ? (j'attends une valeur numérique, rien d'autre ; mais fait attention, l'image est renversée...)


Heu alors c'est -1 parce que si on veut ni l'agrandir ni le réduire il faut que le grandissement fasse 1 ou -1 mais comme l'image est renversée alors c'est négatif. Donc -1

(Relis mon message de 11 h 42 : j'avais donné la réponse  )
)
Maintenant :
Grandissement
L'objet est AB
L'image est A'B'
Tu sais que
Qu'en déduis-tu pour et
Est-ce que cela correspond à nos dessins ?

Je comprends pas comment faire..
Comme tu dis c'est facile mais j'y arrive pas. Je vois pas comment faut faire
Ça alors !
Les deux segments ont même longueur mais sont orientés en sens inverse
A' est bien le symétrique de A par rapport à O