Inscription / Connexion Nouveau Sujet
Optique
Bonjour,
Pouvez-vous m'aider s'il vous plait ?
Enoncé : On place un objet CD mesurant 20cm devant une lentille convergente. La distance entre le foyer objet et la lentille est de 40cm. CD est placé à 100 cm du sommet de la lentille et incliné par rapport à l'axe optique. L'objet forme un angle de 35° avec celui-ci.
1ère question : Est-ce que l'énoncé peut s'écrire ainsi ?
On place un objet CD mesurant 1cm devant une lentille convergente. La distance entre le foyer objet et la lentille est de 2cm. CD est placé à 5 cm du sommet de la lentille et incliné par rapport à l'axe optique. L'objet forme un angle de 35° avec celui-ci.
2ème question : Est-ce que l'objet CD est orienté vers la lentille ?
3ème question : Est-ce que l'image C'D' est orienté vers la lentille ?
Bonjour
Est-ce que l'énoncé peut s'écrire ainsi ?
Non : il faut faire les calculs et les raisonnements avec les valeurs fournies par l'énoncé. Cela ne t'empêche pas de faire une figure soignée "à l'échelle", les distances sur ton schéma étant les distances réelles divisées par 20.
Remarque : peut-être qu'en divisant par 10 seulement, cela donnerait une figure plus grande et plus compréhensible.
La position de l'objet CD n'est pas très bien explicitée par l'énoncé. Il faut je pense considérer CD comme un objet plan réel. Tu peux sans doute imaginer C sur l'axe optique à 100cm du centre optique O de la lentille mince, l'angle entre l'axe optique orienté vers la droite et CD étant
=35°.
Pour l'orientation de l'image C'D', c'est à toi de la déterminer. Le mieux serait sans doute de déterminer l'image C' de C et l'image D' de D. Cela dit, je ne vois pas trop l'intérêt de ce problème, les écrans d'observation étant en général perpendiculaire à l'axe optique.
Oui, à peu près. Voici ce que j'obtiens. A toi de compléter en plaçant l'image C'D'.
PS : tu peux imprimer ce schéma, le compléter en traçant un certain nombre de rayons lumineux particuliers puis le scanner et le poster ici.
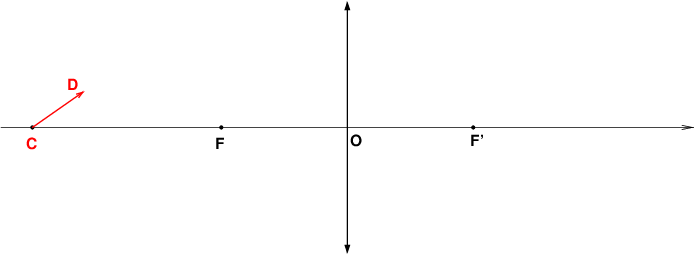
D'accord avec toi pour obtenir graphiquement la position de D'.
Comment as-tu fait pour placer le point C' ?
L'angle doit rester le même que celui qui est dans l'espace objet ?
Cela n'a rien d'évident !
Je te conseille de déterminer l'abscisse de C', par exemple en utilisant la formule de conjugaison de Descartes.
Je trouve une distance OC' d'environ 81,91 cm.
Tu es sûre de ne pas avoir commis d'erreur de signe ?
Là il s'agit dans un premier temps de trouver graphiquement l'image de l'objet.
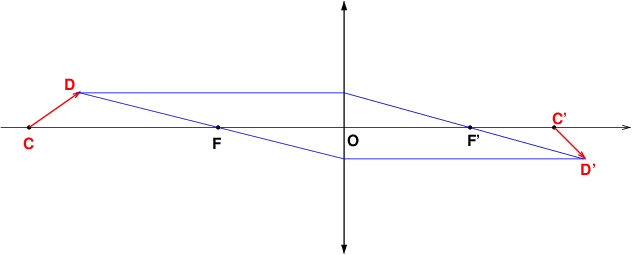
1° un rayon issu de C, confondu avec l'axe optique, n'est pas dévié : cela prouve (ce que tu sais déjà) que l'image C' appartient à l'axe optique.
2° il te faut donc trouver la marche d'un autre rayon quelconque issu de C : le rayon "vert" de mon schéma par exemple. Tu as sans doute étudié en cours comment obtenir la marche d'un rayon ne passant ni par le centre optique ni par un foyer. Tu traces en pointillé un rayon fictif parallèle à celui étudié et passant par O. Ce rayon n'est pas dévié par la lentille. L'ensemble des deux rayons appartient à un faisceau de lumière parallèle, donc les deux rayons vont se couper... où ? Je te laisse réfléchir mais mon schéma fournit "presque" la réponse...
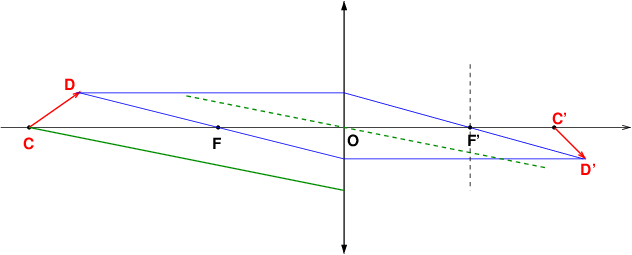
Dans mes calculs, je trouve une valeur différente de l'image que ce qui est représenté sur le schéma, est-ce normal ?
je trouve une valeur différente de l'image que ce qui est représenté sur le schéma, est-ce normal ?
Étonnant ; personnellement, les valeurs calculées sont cohérentes avec les valeurs obtenues graphiquement. Tu peux détailler tes calculs, en particulier celui de la distance OC' ? As-tu réussi à terminer le tracé de mon schéma du 08-10-24 à 23:29 ? Si oui, cela te conduit à quelle valeur de OC' ?
Pour OC, je trouve -86.60cm.
Pour OC', je trouve 74.33cm.
Pour le grandissement, je trouve -0.86.
Donc C'D' = -17.2cm
Est-ce que c'est bon ?
Formule de conjugaison de Descartes :
avec :
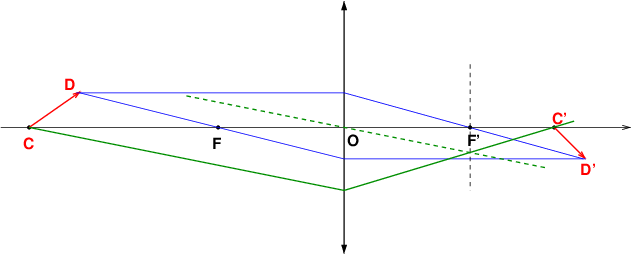
Résultat tout à fait cohérent avec le tracé des rayons issus de C (voir mon schéma complété).
Attention à l'utilisation de la formule du grandissement de ton cours : elle te fournit le grandissement transversal, c'est à dire celui obtenu pour un objet CD perpendiculaire à l'axe optique. Puisqu'il s'agit d'étude graphique, il faut graphiquement obtenir les positions des points C' et D' comme déjà expliqué puis mesurer la distance C'D' en tenant compte de l'échelle. Personnellement, j'obtiens :
C'D'=14,5cm
L'image étant inclinée vers le bas, l'angle entre la direction de cette image et l'axe optique étant de 46,4° (ou -46,4° si tu décides d'algébriser les angles).
PS : n'hésite pas à poser des questions complémentaires si tu n'as pas bien compris la méthode graphique permettant d'obtenir la position de C'.
C'est le mot "sommet" qui prête à confusion. Une lentille convergente est le plus souvent constitué d'un bloc de verre limité par deux surfaces sphériques appelées dioptres et on appelle "sommet" d'un dioptre son intersection avec l'axe optique. Une lentille possède donc deux sommets mais, la lentille étant considérée comme "mince", ces deux sommets sont confondus avec le centre optique O de la lentille. Le mot "sommet" évoquait sans doute pour toi le bord haut de la lentille (la pointe de la flèche sur le schéma).
On a bien ainsi : .
Oui, vous avez raison. Le problème venait de là. Y a-t-il un moyen de trouver le grandissement en faisant un calcul ?
Car en faisant le calcul, on trouve un grandissement entre 0 et -1, ce qui est logique car l'image est inversée et rétrécie.
Pour le grandissement, c'est un peu plus compliqué car tu ne connais que la formule du grandissement transversal. Méthode possible :
1° : obtenir la position du point H, projeté orthogonal de D sur l'axe optique :
avec L=20cm : longueur de l'objet CD
2° : obtenir l'image H' de H en utilisant la formule de conjugaison de Descartes.
PDF - 6 Ko
La moitié du précédent message a été coupé lors de l'envoi... Je reprends donc la fin...
3° déduire la hauteur H'D' de la hauteur HD en utilisant la formule du grandissement transversal.
4° calculer la longueur L'=C'D' de l'image en utilisant le théorème de pythagore.
5° le triangle rectangle (C'H'D') permet de déterminer sin(') puis d'en déduire la valeur de l'angle '.
PS : cela me paraît bien compliqué et de peu d'intérêt au niveau terminale...
L'angle obtenu pour l'image avec l'axe optique doit-être positif ou négatif pour respecter les conventions ?
Quand tu définis le grossissement par une formule du type :
G='/, les angles sont-ils algébrisée ? Pour toi, le grossissement peut-il être négatif ? Il semble que non à lire ton énoncé sur la lunette astronomique. Dans ce cas, laisse la valeur de ' positive sachant que ton schéma indique clairement le fait que l'image est inversée.
Annuler
connectez vous