Bonjour,
j'ai un devoir maison de physique à faire. cependant je rencontre quelques difficultés. merci d'avance pour l'aide et je m'excuse d'avance pour ne pas avoir réussi à copier les images.
(***Lien supprimé*** voici le lien du sujet pour avoir accès aux images car je n'ai pas réussi à les insérer )



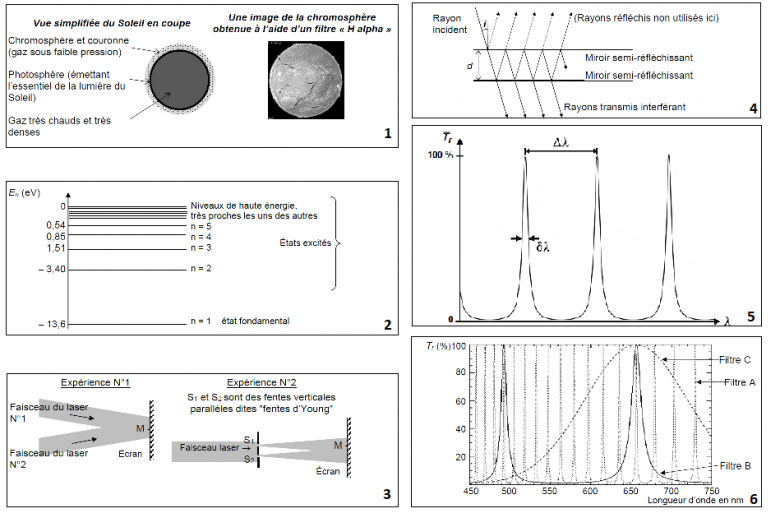
Un filtre solaire « H alpha » est un accessoire pour télescope, permettant notamment
d?observer avec beaucoup de précision les détails de la chromosphère, couche peu dense mais très active de l?atmosphère solaire : protubérances, turbulences, filaments, taches...

(image)

La lumière intense émise par la photosphère empêche un observateur terrestre de
distinguer la chromosphère. Pour pallier cet inconvénient, on utilise des filtres appropriés à
l?observation du Soleil. Les atomes d?hydrogène présents dans la chromosphère absorbent
la lumière émise par la photosphère et la réémettent vers l?extérieur. La longueur d?onde,
sélectionnée par ces filtres, correspond à une raie du spectre de l?hydrogène appelée
H alpha (H). La photosphère est alors invisible et seule la chromosphère apparaît.

Données :
Charge élémentaire : e = 1,602 × 10?19 C
Électron-volt : 1 eV = 1,602 × 10?19 J
Constante de Planck : h = 6,626 × 10?34 J.s
Célérité de la lumière dans le vide : c = 2,998 × 108 m.s?1
1. La raie « H alpha »
1.1. La longueur d?onde mesurée dans le vide de la raie H est = 656,3 nm. En
déduire la fréquence d'une telle radiation.
j'ai trouvé 4.568 * 10^14 Hz

Le diagramme ci-dessous représente les niveaux d?énergie (exprimés en électrons-volts) de l?atome d?hydrogène.

(image)

1.2. Identifier la transition qui correspond à l?émission de la raie H.  
E=Efinale - Einitial = 1.89
on passe donc de n=3 à n=2

2. Filtre interférentiel
On utilise le principe des interférences constructives et destructives pour « sélectionner »
certaines longueurs d?onde au détriment d?autres.
2.1. Obtenir une figure d?interférences
Deux expériences sont proposées pour observer des interférences lumineuses sur un
écran :

(image)

2.1.1. Quelle expérience permet d'obtenir de façon certaine des interférences ?

l'expérience n°2 avec les fentes de Young

Dans l?expérience N°2, des rayons de lumière monochromatique de période T,
provenant d?un faisceau laser, passent à travers deux fentes d?Young S1 et S2 et
viennent interférer sur l?écran. Soit M un point quelconque de cet écran.
La différence de trajet parcouru par les rayons provenant respectivement de S1 et S2
entraîne un retard entre les deux ondes au point M.

2.1.2. À quelle condition, portant sur et T, le point M appartient-il à une frangebrillante ? à une frange sombre ?

constructive frange brillante = KT
destructive frange sonbre
= (2k+1) T/2


2.2. L'interféromètre de Fabry-Pérot

L?interféromètre est constitué de deux miroirs parallèles partiellement réfléchissants,
séparés d'une distance d. En raison des réflexions multiples entre les deux miroirs,
des rayons transmis, parallèles entre eux, sortent de la cavité et interfèrent.

(image)
En raison de la multiplicité des réflexions, seules les radiations dont les longueurs
d?onde vérifient la condition d?interférences constructives seront transmises avec une
forte intensité lumineuse. Lorsque les interférences sont destructives, l?intensité
transmise est très faible.
La figure ci-dessous représente l'évolution du coefficient de transmission en intensité,
Tr, de l'interféromètre en fonction de la longueur d'onde de la radiation incidente.

(image)

On considère une radiation de longueur d?onde qui pénètre dans l?interféromètre sous l?angle d?incidence i, comme indiqué sur la figure ci-dessus.
On admet qu'il y aura des interférences constructives si et seulement si la relation
suivante est vérifiée :
2 d.cos(i) = k. où k est un nombre entier.
2.2.1. Vérifier que si d = 49,88 m et i = 0,000°, les interférences sont constructives
pour la longueur d?onde = 656,3 nm. Préciser la valeur de k.
k=152

2.2.2. Parmi les longueurs d?ondes qui vérifient la condition d?interférences
constructives, déterminer la valeur de la longueur d?onde de la radiation qui précède directement, ou qui succède (au choix), à la radiation de longueur
d'onde .

je suis bloquée à partir de cette question

2.2.3. Calculer alors la valeur de l?écart entre deux longueurs d?onde successives
et vérifier que (?²?)/2d

2.3. Utilisation de l?interféromètre comme filtre
On donne ci-dessous les courbes de transmission (variations du coefficient de
transmission Tr en fonction de la longueur d?onde) de trois filtres notés A, B et C,
utilisés dans un filtre solaire.

(image)

2.3.1. Déterminer la longueur d?onde de la radiation transmise commune à ces trois
filtres. Commenter.

2.3.2. Les filtres A et B sont de type « Fabry-Perot ». Comparer qualitativement leurs
paramètres : distance entre les deux miroirs, nature plus ou moins
réfléchissante des miroirs.

2.3.3. Expliquer brièvement pourquoi il est nécessaire de superposer plusieurs filtres
pour sélectionner correctement la raie H.