Inscription / Connexion Nouveau Sujet
Nucleaire : Compteur Geiger
Bonjour, je planche sur cet autre exercice. Je sollicite votre appui.
Problème
Problème 17
Une source radioactive S était constituée initialement du vanadium . Ce nucléide radioactif est émetteur
 -. Le noyau fils
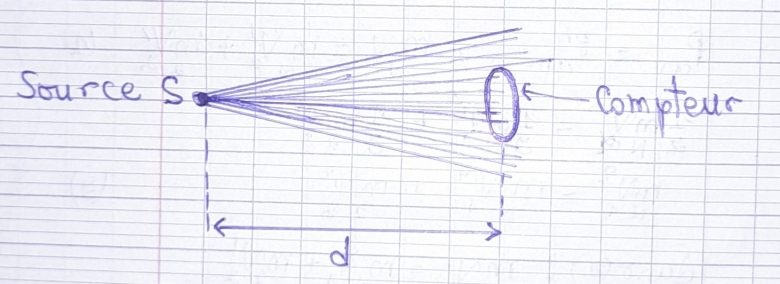
-. Le noyau fils obtenu est stable. La source S, quasi ponctuelle est placée à une distance d = 5 cm de la fenêtre d'un compteur Geiger. La surface de la fenêtre est s = 4 cm². On néglige l'absorption par l'air et on admet que le compteur ne détecte que les électrons émis par la source. On admet que la source émet de la même manière dans toutes les directions.
1) Le compteur évalue le nombre (a) d'électrons qui passe par la fenêtre en 1 s. Après avoir défini l'activité A de la source mesurée en becquerel, montrer que l'on a A = 78,5a.
On donne : surface d'une sphère de rayon R est 4 R².
R².
2) On relève à t = 0 et toutes les 20 s le nombre (a), on trouve la série des valeurs suivantes : 62 ; 58 ; 55 ; 52 ; 48 ; 46 ; 43 ; 40 ; 38 ; 36 ; 33 ; 31 ; 30 ; 28 ; 26 ; 25 ; 23 ; 22 ; 20.
Tracer la courbe représentative de (a) en fonction du temps et en déduire la période radioactive du vanadium 52.
Echelle : 1 cm pour 20 s ; 1 cm pour 5 électrons.
Calculer l'activité A0 à la date t = 0.
Au bout de combien de temps après le début du comptage l'activité A devient-elle égale à 2433 Bq ?
3) Calculer la constante radioactive du vanadium 52. En déduire le nombre de noyaux contenu dans la source au début du comptage.
Question 1)
L'activité A de la source S est le nombre de désintégrations qui s'y produit par unité de temps : A = -dN/dt =  N
N
Or N = N0e- t ; donc A=
t ; donc A= N0e-
N0e- t
t
Soit A=A0e- t avec A0=
t avec A0= N0
N0
Maintenant on me demande de montrer que A = 78,5a.
C'est là que je n'ai pas du tout compris comment aborder la question.
re ,
Non , vous interprétez à votre façon , l'énoncé ( totalement correct ) .
La source émet de façon isotrope ( égale dans toutes les directions ) des électrons . Votre compteur , placé à une certaine distance , ne peut , à cause de sa faible surface d'entrée , n'en compter qu'une petite fraction .Or , l'activité de la source , c'est bien ce qu'elle émet réellement dans toutes les directions à chaque seconde .
Donc , un ( simple ) problème de géométrie dans l'espace .
On vous donne la relation d'une surface de spère ...
En fait , le tout début n'est pas faux , plutôt hors sujet .
Ici , l'activité de la source , c'est ce qu'elle émet dans toutes les directions à chaque seconde .
OK, j'ai compris la définition de l'activité pour ce cas particulier.
Maintenant comment traduire cette définition en expression mathématique ?
Je vais tenter : Où a' est le nombre d'électrons émis.
Or si j'ai bien compris, ce n'est pas le nombre a' qui traverse la fenêtre du compteur Geiger, c'est plutôt le nombre a. Dans ce cas comment lier a' et a à travers une formule mathématique ?
L'activité n'est pas un cas particulier ici .
L'activité , c'est toujours le nombre de désintégrations de la source à chaque seconde ( surnommée : becquerel ).
Ici , comme il y a un électron émis par désintégration , c'est le nombre d'électrons émis par la source à chaque seconde .
Vous compliquez trop . Essayer de " voir " la situation : faites un petit dessin . la source ponctuelle , les électrons , le compteur :
la source émet ses électrons de façon isotrope ( égale dans toutes les directions ), elle émet de façon isotrope en 4 stéradians . Le compteur , petit , ne peut les compter tous ...
stéradians . Le compteur , petit , ne peut les compter tous ...
D'accord merci bien.
Maintenant la surface de la fenêtre est s = 4 cm²
La surface de la source est S = 4 R² ; ici R = d
R² ; ici R = d
Le rapport des surfaces
Où a' est le nombre d'électrons émis par la source S et a le nombre d'électrons reçus par la fenêtre de surface s.
Je ne sais pas si je suis la bonne voie.
On approche ...
Le compteur est situé sur la sphère de rayon d .
tous les électrons traversent la sphère de rayon d , sauf ceux qui entrent dans le compteur .
La source est " quasi ponctuelle " dit l'énoncé , elle n'a pas de surface .
Donc si je comprend bien, je dois dessiner une sphère de centre S, de rayon d et ensuite placer mon compteur de surface s à la distance d de S. C'est ça ?
Oui , car de cette façon , votre compteur est placé sur la surface où la densité des électrons émis est la même en tout point entourant la source . Et à ce moment , une simple comparaison des surfaces ....
Tous les électrons émis par la source ponctuelle et isotrope traversent la sphère de rayon d=5 cm . la surface de cette sphère est de 314.2 cm2 .
Sur cette sphère est placé un compteur de surface 4 cm2 : il ne capte donc seulement 4/314.2 des électrons totaux émis et pour avoir le nombre réel d'électrons émis par la source , il multiplier ce que voit le compteur par 314.2/4 = 78.5 .
Oh merci bien, j'ai passé beaucoup de temps à essayer de trouver cette valeur, mais j'ai pas pu. Merci infiniment.
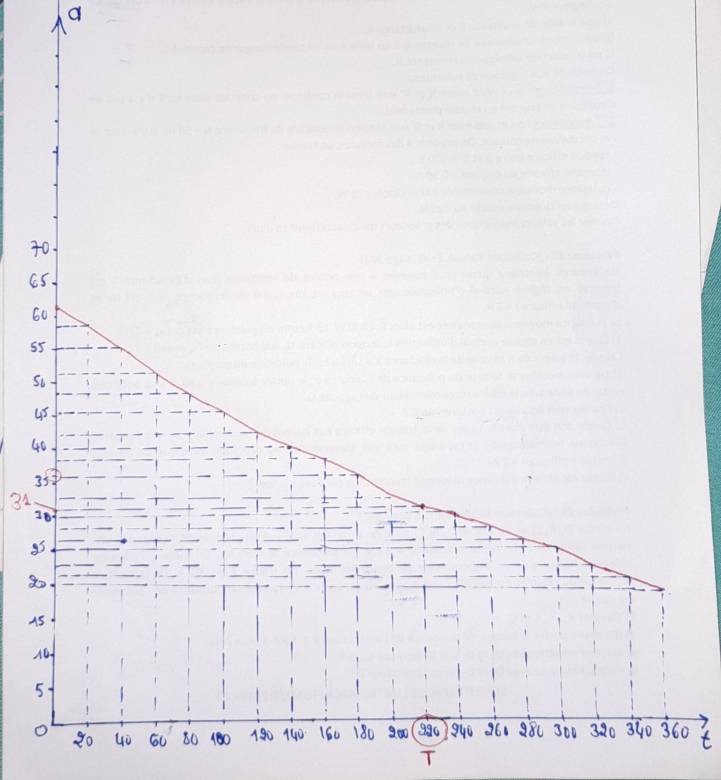
Pour la question 2), il s'agit de tracer la fonction a = f(t). Je vais tenter de le faire minutieusement et ensuite vous allez vérifier pour moi.
Question 2)
Tracé de la fonction a = f(t)
Voir courbe ci-dessous.
- la période radioactive du vanadium 52 est la durée correspondante pour a = 62/2 = 31
Sur le graphe, si a = 31, t = 220 s
Donc T = 220 s
C'est ça ?
Oui , c'est bon .
Vous n'avez pas de papier quadrillé , ça aide ...
les points sont bien choisis : sur 3 portions différentes
de 61.8 à 30.9
de 50 à 25
de 40 à 20
je trouve à chaque fois 220 s !
Merci.
À présent, on demande de Calculer l'activité A0 à la date t = 0.
A un instant t, A = 78,5a
Or à t = 0, a = 62
Alors A0 = 78,5*62 = 4867 Bq
A0 = 4867 Bq
D'accord, j'ai compris.
Au bout de combien de temps après le début du comptage l'activité A devient-elle égale à 2433 Bq ?
À un instant t quelconque : A = 78,5a
Donc si A = 2433 Bq, alors a = 2433/78,5 = 30,99 électrons
Soit a ≈ 31 électrons
Or à t = 0, il y avait a = 62 électrons
Donc pour a = 31 électrons correspond à la moitié de la disparition des électrons initialement présents. Le temps correspondant est la période
Donc t = T = 220 s
Non , vous compliquez . On ne vous demande pas de trouver une période .
on vous demande un temps au bout du quel ...A lire sur la courbe ...
C'est la démarche inverse à la précédente question .
Alors là, je n'ai pas compris cette question.
J'ai cru que si A = 2433 Bq, alors a ≈31 électrons et le temps t demandé est lisible sur la courbe :
t = 220 s
Merci bien
Donc N = A/
Au début du comptage a = 62 électrons, donc A = 78,5*62 = 4867 Bq
AN : N = 4867 / (3,15.10-3)
N = 1,54.106 noyaux



