Inscription / Connexion Nouveau Sujet
Notion d'énergie potentielle
Bonjour,
J'ai un petit problème concernant l'énergie potentielle. C'est l'histoire des signes qui me donne des ennuis.
Voici un petit exercice concernant le sujet
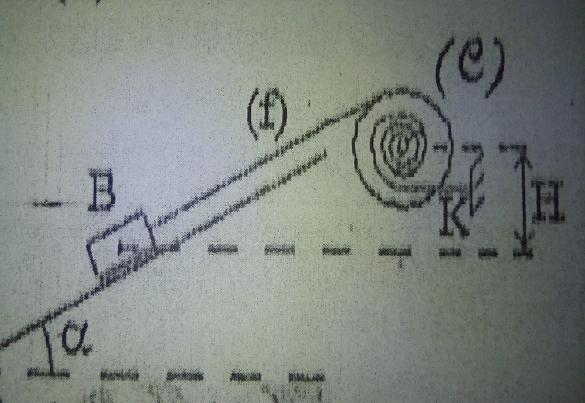
Un corps B de masse M=1kg peut glisser sans frottement sur le plan incliné faisant un angle
=30° avec l'horizontale. Un fil (f) inextensible, de masse négligeable et parallèle au plan incliné, relie le corps B au cylindre (C) de masse m=M et de rayon r=0,1 m. Une partie du fil est enroulée autour du cylindre (C). Une extrémité d'un ressort spiral de constate de torsion C=0,49 mN/rad est soudé en un pt de la base de (C).
(C) peut tourner autour de son axe de révolution (
).
1) Calculer l'angle 
0 du ressort spiral lorsque le système {corps B+cylindre (C)+ ressort spiral} est en équilibre.
2) On écarte le corps B vers le bas à partir de sa position d'équilibre et on l'abandonne à lui-même
a) en prenant l'énergie potentielle de pesanteur nulle à la position du corps B à l'équilibre, montrer que à un instant t, l'énergie mécanique du système s'écrit :
H est la distance entre les plans horizontaux passant par les centres d'inertie de B à l'équilibre et du cylindre (C).
b) établir l'équation différentielle du mouvement du cylindre
(C) autour de son axe de révolution. Calculer T, sa période
1) Calcul de 0
J'ai découpé système par système et au final j'obtiens la condition d'équilibre du système
C0-Mgrsin
Et 0=1,02°
2)a) Em=Ec+Epp+Ep torsion
=(1/2) J.²+(1/2) mV²-mgx sin+(1/2) C(+0)²+ mgH
J'ai au début écrit mg x sin car la hauteur z est variable mais ça n'a pas renvoyé à la condition d'équilibre
Je ne comprends pas
Pouvez vous m'éclairer svp
Bonjour,
Je pense que :
Epp = M g x sin (α) + M g H
x = r θ
Epp = M g r θ sin (α) + M g H
Or M g r sin (α) = C0
Epp = C0 + MgH
Epe = (1/2) C(-0)²
Après développement et simplification :
Epp + Epe = (1/2) C (-0)² + MgH
Autre chose ...
Question 1 :
Je suppose que la valeur de "g" attendue est ici de 9,8 m/s² qui se simplifie parfaitement avec le 4,9 mN/rad
On obtient alors un angle 0 de 1,0 .... radian et pas 1,0 degré !
Mais là n'est pas mon problème, loin de là
C'est le signe de l'énergie potentielle de pesanteur qui me chiffonne.
En fait, je n'ai pas eu le temps de questionner mon prof.
Svp aidez moi
Si je n'ai pas fait d'erreurs dans mon calcul ( 10-09-19 à 19:25 ) le signe de l'énergie potentielle de pesanteur comme celui de l'énergie potentielle élastique est imposé par la valeur elle même positive ou négative de
J'ai bien compris que " là n'était pas ton problème", tant s'en faut.
Mais je tiens tout de même à rectifier une sottise que j'ai commise par inattention dans mon denier post au sujet de l'énergie potentielle élastique :
En effet, contrairement à l'énergie potentielle de pesanteur l'énergie potentielle élastique est toujours positive.
L'énergie potentielle de pesanteur n'est pas toujours négative.
Son signe dépend de la position du corps étudié par rapport au niveau de référence.
Si le corps est au dessus du niveau de référence son énergie potentielle de pesanteur est positive, sinon elle est négative.
Si le corps étudié oscille de part et d'autre du niveau de référence son énergie potentielle de pesanteur est alternativement positive et négative.
L'énergie potentielle de pesanteur du système {B + C} est la somme de deux termes :
Epp = M g r θ sin (α) + M g H
Je ne vois pas sur quoi tu t'appuies pour affirmer (sans démontrer) que cette énergie potentielle de pesanteur est toujours négative.
Oui MgH>0 car c'est en haut du référence
Mais c'est pour B que ça se gâte
En effet son Eppest tantôt positif tantôt négatif
Mais regardez
La condition d'équilibre est
C 0-Mg r sin
Je suis sensé avoir cela dans l'expression de Em pour avoir l'expression demandée
Je n'obtiens pas si l'Epp de B est Mgr sin
Il faut qu'elle soit négative.
Je m'emêle tout le temps dans ce truc à chaque fois qu'il demande de trouver l'Emdu système
Svp, pouvez vous m'expliquer?
Il me semble bien avoir déjà fait ce calcul dans mon post du 10-09-19 à 19:25
Epp(B) = M * g * x * sin (α)
x = r * θ
Epp(B) = M * g * r * θ * sin (α)
A l'équilibre on a : M * g * r * sin (α) = C * θ0
Il en résulte que :
Epp(B) = C * θ0 * θ
C et θ0 sont des constantes, mais θ est une variable qui ici est alternativement positive et négative tout comme Epp(B)
Et comment est-ce qu'il disparait le C0 dans l'expression de l'énergie potentielle que vous avez postée (10-09-19 à 19:25)?
J'ai aussi expliqué cela (10-09-19 à 19:25 avec rectificatif 10-09-19 à 19:41)
Je détaille le calcul :
Epe (de torsion) = (1/2)C( θ - θ0)² = (C/2) (θ² + θ0²) - C θ θ0
Epp = C θ θ0 + M g H
Ep = Epe + Epp = (C/2) (θ² + θ²0) + MgH
Annuler
connectez vous