Inscription / Connexion Nouveau Sujet
mvt parabolique champ de pesanteur
salut je suis bloque et je sollicite votre aide
Un projectile considéré comme ponctuel est lancé, dans le champ de
pesanteur, à partir d'un point A situé à la distance h = 1 m du sol,
B
avec une vitesse faisant un angle a avec l'horizontale et de valeur Vo =16 m.s-1.
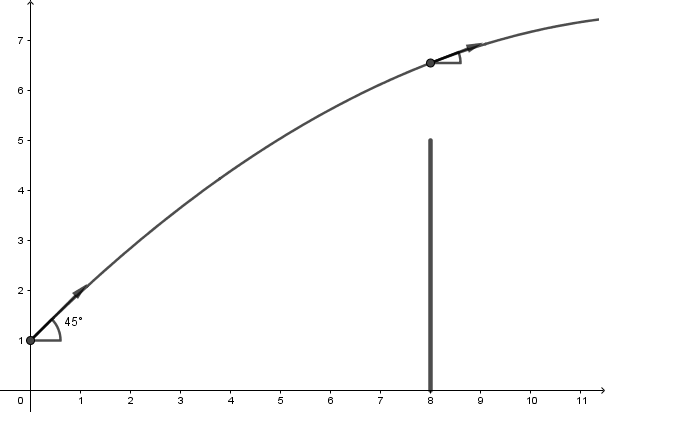
Un mur de hauteur H = 5 m est disposé à la distance L = 8 m du lanceur.
D
Il Etablir l'équation du mouvement du projectile dans le repère (0, 1,j).
21 Etablir l'équation cartésienne de la trajectoire du projectile. Quelle est sa nature?
31 Entre quelles valeurs doit être compris l'angle a pour que le projectile
1 H = 5m
A
passe au-dessus du mur?
4 1 On fixe la valeur de a à 45°.
al Soit B le point de passage du projectile au-dessus du mur
Calculer la distance d séparant le sommet du mur au point B.
L=8m
bl Soit Ve la vitesse du projectile au point B.
Notons~ l'angle formé par la vitesse Vs et l'horizontale~= (Ox ,Vs). Calculer~-
cl Calculer l'altitude maximale Y max atteinte par le projectile. Déterminer la portée X du tir
1/y=-0,02x^2)/cos(alpha)^2+xtan(alpha)+1 elle est parabolique
2/il faut qu Y(L)>H alors alpha est compris entre 36,5 et 80 degres
3/ d=Y(8)-5 , d=1,44m
b/calculer beta
d'apres le tec entre h=1 et h=6,44 j'ai Vb=12,13ms
x(t)=12,13cos(Beta)
y(t)=-5t^2+Vbsin(beta)+6,44
je ne sais plus continuer
Désolé, j'ai posté trop vite :
Un des moyens de trouver la valeur de l'angle 
Attention aux erreurs induites en transportant des arrondis d'un calcul à l'autre.
En prenant g=9,8m/s² J'ai trouvé que le projectile passait 1,55m au dessus du mur là ou tu trouves 1,44m
heuu l'exo m'a impose g=10 de plus je connais ce que t'as poste mais je me demande bien comment l'exploiter
Avec g= 10m/s² je trouve 1,50m
Tu as calculé la valeur de V
Tu calcules celle de Vx
Puis celle de Vy
Puis celle de tan( ) donc de
) donc de 
Vb=12,13 relis mon tout premier post j'ai utilise le TEC
vx et vy je connais leur expressions mais rien de plus
C'est bien parce que je sais que tu as calculé Vb = 12,13 m/s que je t'ai proposé cette méthode.
Tu sais que Vx = V0*cos( )
)
L'énoncé donne V0 = 16m/s et  =45°
=45°
Rappel : Vx est constant
Connaissant Vb et Vx le théorème de Pythagore te permet de calculer Vy
Connaissant Vx et Vy on accède à tan( ) puis à
) puis à 
vy^2=Vb^2-Vx^2=147,2-16^2cos9450^2=19,2 alors vy=4,4ms-1
tan=vy/vx=4,4/12,3=0,35 donc
 =19,29degres
=19,29degres
si l'altitude est max alors Vy=0
Vy=-10t+11,31 , vy=0 alors t=1,31s
y(1,31)=Hmax=7,2356m
Sur le plan théorique, tu as bien trouvé les réponses aux diverses questions.
C'est le principal.
Sur le plan numérique, je ne trouve pas les mêmes résultats que toi.
Tu as (une ou plusieurs) erreur(s) d'étourderie comme quand tu écris que l'équation
-10t+11,31=0 a pour solution t=1,31s
Tu as surtout (et c'est plus ennuyeux) des erreurs de méthode en propageant des arrondis obtenus dans des calculs intermédiaires. Les erreurs d'arrondis s'accumulent et peuvent finir par fausser les résultats.
La meilleure méthode consiste à mener des calculs littéraux et à ne faire l'application numérique qu'à la fin.
Si, malgré tout, tu es amené à utiliser des résultats numériques intermédiaires il faut alors leur conserver la plus grande précision possible.
Je te donne, (pour comparaison) mes résultats obtenus en utilisant g=10m/s² et exprimés avec 3 chiffres significatifs.
y(8)=6,50m
Distance entre le sommet du mur et le projectile : 1,50m
Vitesse du projectile au point B : 12,1 m/s
Angle β = 20,6°
Altitude maximale : 7,40m
Portée : 26,6m
Et je suis bien conscient que je ne suis pas, moi aussi, à l'abri d'une ou plusieurs erreurs.
Angle β = 20,6°
Altitude maximale : 7,40m
Portée : 26,6m
je peux voir ton application numerique sur ces resultats stp
J'ai obtenu en (m/s)²
En appliquant le théorème de l'énergie cinétique entre le point de départ et le sommet de la parabole j'obtiens que le dénivelé H entre ces deux points est tel que :
H = (16² - (16*cos(45°))² / ( 2 * 10 ) =(16²-128)/20=6,40m
Le point de départ étant situé à 1m au dessus du sol l'altitude maximale est 6,40 + 1,00 = 7,40m
L'équation cartésienne de la parabole s'écrit :
y(x) = -(5/128)x²+x+1
On cherche la valeur de x pour qui y(x) = 0
La racine positive de cette équation est x=26,6m
merci maintenant tu peux repondre au sujet que j ai recemment poste nomme : dynamique de newton , mvt rectiligne puis circulaire
Il n'est pas très correct de solliciter une aide depuis un topic vers un autre topic.
Sans compter que tes énoncés sont de moins en moins lisibles.



