Bonjour,
On choisit comme origine des espaces le point ou se trouve la voiture à la date t=0
On choisit comme origine des dates l'instant ou la voiture démarre.
Avec ces choix : x(t) = (1/2)*a*t²

Calcule d'abord l'accélération " a " de cette voiture.
La "troisième seconde" débute à la date t=2s et se termine à la date t=3s
La distance D cherchée est donnée par D = x(3) - x(2)

Donc la position initiale est 0m? Je ne comprends pas très bien..
La position finale est 150 m. On sait aussi que la vitesse initiale est 0m/s et le temps = 15sec.. mais la position initiale.. on n'a pas de donnée sur ça..

Equation générale d'un MRUV : x(t) = (1/2)*a*t² + v(0)*t + x(0)
Ici on a v(0) = 0 et x(0) = 0

donc, comme indiqué précédemment : x(t) = (1/2)*a*t²
L'énoncé indique que x(10) = 150m
donc :
150 = (1/2)*a*(10²)
150  = 50 * a
a = 3m/s²

Je te laisse terminer.

Ah oui d'accord..
Pour x(3) j'ai trouvé 13,5m tandis que pour x(2) : 6m. La différence me fait 7,5m.

Mais en fait il y a quand meme une chose que j'ai du mal à saisir, et ce depuis longtemps déjà.
Ici x(0) =0, cela veut dire que la position lorsque t=0sec vaut 0m?
Mais ça ne peut pas exister par exemple, une position initiale qui n'est pas nulle alors que le temps et la vitesse initiale sont tous les deux nuls?

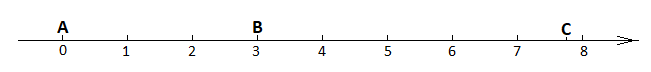
Je dirais que pour X1(t) = Xo + 4*0^2/2 donc x1(t) = xo (ça me parait faux)
Tandis que pour x2(t) = xo + 3*3^2/2 donc x2(t) = xo + 13,5

Pour (1) :
x₁(t) = (1/2)*4*t² = 2t²
En effet à la date t=0 le mobile ( 1) se trouve en A à l'abscisse x(A) = 0

Pour (2) :
x₂(t) = (1/2)*3*t² + 3= 1,5t² + 3
En effet à la date t=0 le mobile (2) se trouve en B à l'abscisse x(B) = 0

Tu vois donc que pour B il est parfaitement possible qu'un mobile se trouve à :
une position initiale qui n'est pas nulle alors que le temps et la vitesse initiale sont tous les deux nuls

Entraîne toi :
Je ne change rien aux données précédentes mais je modifie l'origine des espaces sur l'axe A BC

Que deviennent les équations horaires de (1) et de (2) ?

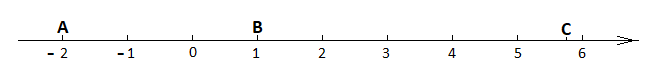
Attention à ma faute de frappe concernant le mobile (2) :

En effet à la date t=0 le mobile (2) se trouve en B à l'abscisse x(B) = 3

Pour X1(t) = -2 + 2t^2
X2 (t) = 1+3t^2/2

Parfait.

Cette fois ci les deux mobiles (ayant tous les deux une vitesse initiale nulle) ont une abscisse non nulle à la date t=0

Conclusion : La valeur x(0) de l'abscisse à la date t=0 dépend du choix de l'origine des espaces.

D'accord, merci beaucoup pour ces explications.

Donc lorsque j'ai x(0), en français ça va se lire, la position au temps t=0s, ça veut dire que le mobile n'a pas encore commencé à bouger mais si ça tombe dans l'énoncé la position initiale n'était pas à 0m... je suis encore de nouveau perdue

Dans l'énoncé on dit juste que le mobile part du repos, donc cela veut dire la vitesse initiale= 0. Donc on aura V(0) = 0 car t=0 mais alors puisqu'on a montré que la position initiale peut etre différente de 0 meme si la vitesse et le temps sont tous les deux 0, comment on sait dans cet exercice que la position initiale c'est 0?
Je suis désolée, je bloque sur qqch de très stupide je sais..

Mais en fait c'est comme si on représentait un graphe de x(t) et on traçait  une parabole qui touche l'axe des x(t). A cet endroit là ça veut dire que t=0, mais x aura une valeur c'est ça?

Je suppose que tu fais référence à un MRUV, sinon il n'y a aucune raison que la représentation graphique de x(t) soit une parabole.

Le point d'intersection de la parabole avec l'axe des ordonnées est en effet x(0) c'est à dire la position du mobile à la date t=0

D'accord.

Donc comme vous avez dit, puisque la personne qui résout l'exercice doit choisir un repère (si le l'énoncé ne l'impose pas), nous on a choisi que à v=0, x(0) = 0, c'est ça?

Je suppose que tu as voulu dire qu'on a choisi que x=0 à la date t=0 ce qui s'écrit aussi x(0)=0 et parfois aussi x₀=0
C'est en effet un choix qu'on fait très souvent car il simplifie l'équation horaire.
Ce choix fréquent est parfois désigné par l'expression " origines qui coïncident" (origine des espaces qui coïncide avec l'origine des dates)

D'accord.

Mais si l'énoncé avait précisé que par exemple Xo = 100m, dans ce cas on aurait plus le droit de le faire nous meme?

C'est cela même !
Imposer X₀ = 100m revient à choisir une origine des espaces telle que X(0)=100m c'est à dire que le mobile
( en mouvement ou non ) se trouve au point d'abscisse 100m à la date t=0

D'accord.

Merci beaucoup