Bonjour, nous avons un exercice à rédiger pour vendredi dont voici les documents et les questions. J'ai répondu aux questions mais je n'en suis pas sure, et donc j'aimerai avoir une correction à mes réponses fausses.

Voici les documents :

Document 1 : Apesanteur ou impesanteur ?
Ces deux termes ont pratiquement le même sens, mais dans le langage parlé il y a confusion phonétique possible entre la « pesanteur » et l'« apesanteur » d'ou l'utilisation du mot « impesanteur » lorsqu'il y a absence apparente de pesanteur.
Un objet est en apesanteur lorsqu'il y a absence totale de pesanteur (concept théorique).
Supposons par exemple un objet placé dans une cabine en chute libre :
-          dans le référentiel terrestre, cabine et objet sont tous deux en chute libre et la cabine n'exerce aucune action sur l'objet lui-même et celui-ci « flotte » dans l'air de la cabine.
-          dans un référentiel lié à la cabine, l'objet ne semble pas soumis à la pesanteur, il est en état d'impesanteur.
Un objet est en impesanteur lorsque le sol ou le support n'exerce aucune action sur lui. C'est le cas lors d'une chute libre sous la seule action du poids.  L'impesanteur est donc l'absence relative de pesanteur.
On peut réaliser l'état d'impesanteur de différentes façons :
-  dans une tour de chute libre (durée d'impesanteur de 2 à 10 secondes, selon la hauteur)
-  dans des avions en vol parabolique (durée d'impesanteur de l'ordre de 20 à 25 secondes)
-  dans des fusées sondes (durée d'impesanteur d'environ 6 minutes)
-  dans une station orbitale tournant autour de la Terre (impesanteur permanente).

Document 2 : Pourquoi un vol parabolique ?
Lorsqu'on lance un objet en l'air, hormis le cas où il a été lancé rigoureusement à la verticale vers le haut, sa trajectoire est une parabole. Il s'agit d'une chute libre avec vitesse initiale. Un objet placé à l'intérieur est donc en impesanteur.
Si un avion arrive à effectuer une trajectoire parabolique, passagers et matériel embarqué seront en impesanteur. A noter que dans un "grand-huit", le profil de la piste est conçu pour procurer  cette sensation aux amateurs, en certains points du circuit...
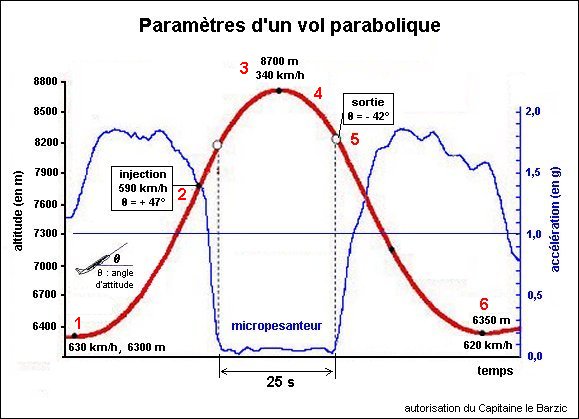
L'Airbus « Zéro G » (*) qui est en vol horizontal à 6300 mètres d'altitude monte en se cabrant à 47 °. Il est alors en hyperpesanteur à 1,8 g (1 g correspond à l'accélération de la pesanteur à la surface de la Terre). Le pilote diminue ensuite la poussée des réacteurs de façon à juste compenser le frottement de l'air et l'avion entre en phase de chute libre dès 8000 mètres. Son contenu est en impesanteur. Son élan lui permet d'atteindre 8 700 mètres puis il retombe (phase descendante de la parabole). Après avoir remis les gaz à 8 000 mètres et retrouvé une phase d'hyperpesanteur l'avion reprend son vol horizontal à 6 300 mètres. L'opération dure environ une minute pour obtenir 25 secondes d'impesanteur ou micropesanteur intercalées entre deux périodes d'hyperpesanteur.

Document 3 : voir image

Document 4 :

L'ISS est le laboratoire le plus grand et le plus sophistiqué à avoir jamais pris la voie des airs. Ses modules équipés spécialisés à l'instar du laboratoire Columbus de l'ESA permettent aux scientifiques d'étudier un vaste éventail de sujets dans un milieu très spécial où tout est en impesanteur. Si, sur Terre, la gravité influence fortement tout ce que nous faisons, des choses très bizarres se produisent quand les effets de cette force disparaissent.
Par exemple, la flamme d'une bougie a pour nous une forme pointue familière. Cette forme allongée vers le haut est due à la montée des gaz chauds, plus légers que l'air frais qui les entoure. L'air froid est attiré vers la base de la mèche et fournit l'oxygène qui entretient la combustion de la cire de la bougie. Mais en impesanteur, les gaz chauds ne sont pas plus légers que l'air froid et rien ne s'élève. Résultat, la flamme est petite et ronde, presque invisible. La combustion proprement dite ne se développe qu'à la surface de la flamme, où le combustible que constitue la cire peut se mélanger à l'oxygène de l'air extérieur.
Observer comment se passe la combustion en impesanteur permet aux chercheurs d'apprendre beaucoup de choses. Ces connaissances peuvent ensuite être utilisées pour, par exemple, concevoir des moteurs de voiture ou d'avion qui consomment moins et polluent moins.
Un autre domaine de recherche intéressant est le mélange des liquides. Bon nombre des métaux que nous utilisons tous les jours sont des alliages, c'est-à-dire des mélanges composés de deux métaux ou plus. Les alliages s'obtiennent en faisant fondre les métaux pour qu'ils se mélangent. Sur Terre, la pesanteur a une forte influence sur la façon dont les différents métaux liquides se mélangent et les mélanger est bien plus simple dans l'espace. Les expériences en impesanteur peuvent nous fournir beaucoup d'informations sur ce procédé et nous permettre de fabriquer de meilleurs alliages de retour sur Terre.

Et voici les questions:

1) Schématisez la situation décrite dans le document 1 en faisant apparaitre les forces mises en jeu.
2) Expliquer pourquoi le spationaute est en état d'impesanteur.
3) On étudie le mouvement parabolique de l'avion que l'on assimile à un point M, dans un repère orthonormé O, . Celui-ci débute à t=0, à une altitude h = 8200 m à la verticale du point O avec un vecteur vitesse v0 faisant un angle = 47° avec l'horizontale. Le champ de pesanteur est supposé uniforme. On prendra g=9,8m.s-2
3)1. Que doit vérifier l'avion pendant la phase d'impesanteur et pourquoi ?
3)2. Quelle est la nature de la trajectoire de l'avion pour obtenir l'effet d'impesanteur pendant le vol ?
3)3. En vous aidant de vos connaissances sur la propulsion, expliquer ce qu'est la poussée des réacteurs. Vous pourrez vous aidez d'un schéma
3)4. On étudie le système avion dans le référentiel terrestre que l'on suppose galiléen.
a.Quelles sont les forces agissant sur l'avion au cours de cette phase ?
b. Déterminer le vecteur accélération en appliquant la 2ème loi de Newton.
c. En déduire les équations horaires du mouvement.
d. Montrer que l'équation de la trajectoire s'écrit : z=- 1/2 g (x/vo *cos alpha) +tan * x+h.

4) Retrouvez la hauteur maximale de vol de l'avion
5) Déterminer le temps ts pour lequel l'avion atteint son altitude maximale.
6) Retrouvez la durée maximalet durant laquelle il est possible d'être en impesanteur par ce procédé.

Mes réponses :
1) j'ai fait le schéma
2) en impesanteur car il effectue une chute avec la station orbitale vers la Terre. Or il ne va pas s'écraser puisqu'il a une vitesse et une accélération tangentielle. ( mais je ne sais pas comment développer plus cette réponse qui me semble fausse )
3)1. L'avion doit vérifier que la poussée des reacteur ne soit pas trop forte et compense la force de frottements afin que l'avion et les passagers ne soient soumis qu'à leur poids
3)2. une trajectoire parabolique
3)3.Je ne sais pas trop, on m'a conseillé d'utiliser la troisieme loi de newton mais je ne vois pas en quoi.
3)4. a)bilan des forces exterieures : poids ( pas de frottements)
b) j'ai trouvé que vecteur accélération est -9,8
c) j'ai trouvé x(t)=cos * v0 * t+x0 avec x0 = 0
et y(t) = -g *(t²/2)+ sin * v0 *t +y0 =
d)je n'y arrive pas non plus
4) je n'ai pas trouvé, ne connaissant pas vo ...
5) ne connaissant pas vo je n'ai pas pu faire cette question...
6) idem...

Merci pour vos aides et vos conseils qui me feront progresser à coup sur pour cette année du baccalauréat