Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

Mouvements d'un système, accélération d'un proton

Posté par
Raph26350 17-03-20 à 13:25

Bonjour, je suis bloqué depuis hier sur un exercice de physique concernant le chapitre "mouvement d'un système", voici l'énoncé:
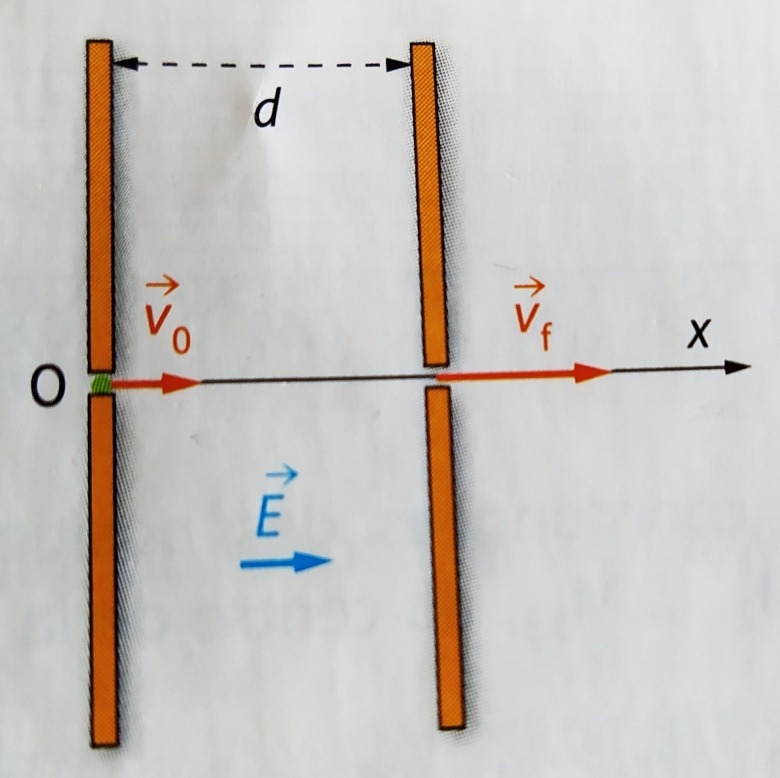
Un proton pénètre dans un accélérateur linéaire de particule avec une vitesse initiale v0 (vecteur vitesse) perpendiculaire aux armatures du condensateur plan.
Un champ électrostatique uniforme E (vecteur) règne entre les deux plaques du condensateur.
Donées: charge du proton e=1.6.10-19 C
masse du proton m=1.7.10-27 kg
vitesse horizontale initiale v0 =4.0.103 m.s
valeur du champs électrique E=2.5 kV.m-1

Les questions:
1. En supposant que le poids du proton est négligeable, donner les caractéristiques de la force F(vecteur) qui modélise l'action mécanique appliqué au proton. (je ne vois pas vraiment les caractéristiques possibles à part la vitesse sachant que le poids est négligeable)
2. En appliquant, sur l'axe horizontal, la relation approchée entre la somme des forces et la variation de vitesse, établir une expression de \deltat
en fonction de m,e,E et \deltav.
3.Pendant combien de temps le proton doit être soumis au champs éléctrique pour que sa vitesse finale vf soit multipliée par 4.

Je suis vraiment perdu, si vous pouviez m'aider, ce serait super.
Merci d'avance.

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 13:56

Bonjour,

Je te souhaite tout d'abord la bienvenue sur le forum !

L'idée n'étant pas de faire l'exercice à ta place, je te propose dans un premier temps d'étudier la fiche suivante, en particulier les § sur la force électrostatique et sur le champ électrostatique (clique sur la maison) : [lien]

Ensuite, il est primordial de commencer par un schéma de la situation, représentant toutes les données fournies par l'énoncé :

attentionextrait de c_faq la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?



Par exemple, le schéma du condensateur plan en fin de fiche pourrait être un bon début ...

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 14:03

Tout d'abord, merci de votre réponse rapide, ensuite, un schéma est déjà disponible sur le manuel, mais je ne peut vous le montrer, faute de moyens, et enfin le but n'est pas que vous fassiez l'exercice à ma place bien entendu, mais de le résoudre pas à pas,  comme dit sur le sujet, j'ai essayé de faire la première partie, et je voulais savoir si au moins un élément de réponse était présent, et si il en manquait, de me le dire, afin que je puisse le trouver, et vous demander si ma nouvelle réponse correspond ou non.
Merci par avance de votre aide

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 14:37

Oui, pour cela il va falloir que tu postes ce que tu as déjà fait.

Je t'ai fourni un raccourci pour t'expliquer comment procéder

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 15:00

D'accord, je vous joint donc le schéma, pris en photo avec les moyens du bord. C'est à cause des mesures qui ont été prises concernant le confinement que je m'en remet à vous, mon professeur n'étant pas disponible.

Concernant les exercices, la première partie me pose problème car je ne sais pas quel(s) vecteur(s) ou donnée(s) utiliser, je sais que d'après mon cours le vecteur "force résultante" est d'une addition de vecteurs force sur l'objet, mais je ne sais pas si c'est applicable ici, car je ne vois pas comment.

Ensuite, pour la deuxième partie, je ne vois pas comment trouver \Delta t
sachant que j'ai des valeurs que je ne sais pas comment manipuler pour atteindre mon but, c'est à dire E et e. Je connais la formule qui lie la masse, \Delta t et \Delta v pour donner la force, mais je ne sais pas comment associer E et e.
Peut être même que ça n'a rien à voir.
Je suis donc plutôt perdu concernant cet exercice, si vous pouviez m'aider à le résoudre au fur et à mesure, ce serait parfait.

Mouvements d\'un système, accélération d\'un proton

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 15:19

Ok, avant d'aller plus loin, je pense qu'il va falloir reprendre les bases et que tu lises attentivement cette fiche de cours : [lien]

et également celle sur les interactions fournie dans mon message du 17-03-20 à 13:56.

Dès que tu seras plus à l'aide avec ces notions, on pourra commencer dans de meilleurs conditions.

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 16:07

Je viens de relire et de comprendre mon cours, celui que vous me proposez ainsi que d'autres cours sur internet, bien qu'en ayant compris ces cours, je ne vois toujours pas comment aborder mieux cet exercice, la seul rectification que je peux faire, c'est que la force résultante correspond à 0 normalement, donc ce n'est pas l'idée prononcé plus haut qui pourra résoudre ce problème, dans ce cas, laquelle ?

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 16:49

Reprenons les bases en mécanique, peux-tu déjà commencer par répondre aux questions suivantes :
* système ?
* référentiel d'étude ?
* bilan des forces appliquées au système ?
* loi ou relation susceptible d'être appliquée ?

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 19:04

J'imagine que le système étudié correspond à l'accélérateur linéaire de particules, comprenant le proton, d'après le cours, nous sommes dans le référentiel Galiléen, concernant les forces, il y a la vitesse v0(vecteur), la vitesse vf (finale) et le champ électrique E(vecteur), les relations possibles sont la variation de vitesse, après je ne vois pas comment appliquer le tout (je ne sais même pas si c'est juste)
Merci de votre aide

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 19:47

Houlà, il faut vraiment que tu prennes le temps de réviser les fiches fournies, tu confonds un vecteur et une force .

Un vecteur vitesse : Représentation et variation d'un vecteur vitesse

Une force : Modélisation d'une action par une force

* Le système qu'on étudie est le proton de masse m et de chaque électrique e, assimilé à un point matériel (cf. définition dans les fiches) ;

* Le référentiel est le laboratoire, référentiel terrestre supposé galiléen

* Bilan des forces appliquées au système :

- le poids du protons \vec{P} de valeur P = m.g qu'on néglige dans cet exercice ;

- la force électrostatique \vec{F_e} exercée par le champ électrostatique \vec{E} : \boxed{F_e = e \times \vec{E}} d'après la fiche de cours.

* Schéma de la situation :

Il suffit de représenter les deux forces qui s'appliquent sur le système.

* D'après la deuxième loi de Newton approchée (cf. la fiche) ...

Relation à trouver dans la fiche et à projeter sur un axe à définir sur ton schéma ...

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 20:00

D'accord, dans ce cas, pour les caractéristiques de la force qui modélise l'action mécanique appliqué au proton, il s'agit de la force électrostatique, et pour la relation de la somme des forces, il faut donc prendre en compte le poids du proton ?
Merci pour votre réponse complète

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 20:50

Pour que tu puisses t'en convaincre, calculons la norme (ou la valeur) de ces deux forces :

* P = m x g = 1.7.10-27 x 9,81 = ... N

* Fe = e x E = 1,6.10-19 x 1,5.103 = ... N

Tu dois constater que P << Fe.

Après, tu peux malgré tout en tenir compte dans ton bilan des forces appliquées sur le proton, puis en appliquant la deuxième loi de Newton approximée, projetée sur l'axe (Ox), elle va se simplifier ...

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 17-03-20 à 21:13

D'accord, merci pour votre aide, je vais appliquer ça de suite

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 17-03-20 à 21:18

ça marche, pense au pouvoir infini des fiches de mécanique (seconde et première) du forum

Je regarderai ta proposition demain matin, bonne soirée !

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 10:09

Voici pour la première question,

1.P ⃗=mg ; donc P ⃗= 〖1,7.10〗^(-27)*9,81=〖1,7.10〗^(-26) N
(F_e ) ⃗=e x E ; donc (F_e ) ⃗= 〖1,6.10〗^(-19)*〖2,5.10〗^3=〖4,0.10〗^(-16) N
Donc  P ⃗≪(F_e ) ⃗
(F_e ) ⃗ modélise donc la force mécanique appliquée au proton F ⃗ qui est rectiligne uniforme et vaut 〖4,0.10〗^(-16) N.

Pour la deuxième, il faut, pour pouvoir calculer \Deltav, faire la somme des forces (mais ce n'est pas ce que l'on vient de faire ?) ou il y une autre méthode (plus précise), car c'est ce que je vois dans le cours concernant la la relation approchée entre la somme des forces et la variation de vitesse...
Merci de votre réponse

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 10:17

problème lors de la frappe pour l'exercice, ce symbole est apparu:〖, il faut l'ignorer

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 10:56

Tu as des utilitaires sur le forum pour faire des formules proprement :

attentionextrait de c_faq la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?



Si je te donnes des liens vers des fiches de cours ce n'est pas pour qu'elles servent de décoration

* Caractéristiques du poids d'un solide : Modélisation d'une action par une force

* Caractéristique d'une force électrostatique et non mécanique) : [lien]

OK avec des applications numériques.

Ensuite, il faut applique la deuxième loi de Newton approchée, cette fiche t'explique cette loi : [lien]

Citation :
Au cours du mouvement d'un système de masse m, la variation de vitesse \Delta \vec{v} de son centre de masse et la résultante \sum \overrightarrow{F} des forces appliquées sont reliées à tout instant par la relation approchée suivante:

\boxed{\sum \overrightarrow{F} \approx m \dfrac{\Delta\overrightarrow{v}}{ \Delta t}}

Cette loi n'est toutefois valable que si le référentiel choisi pour l'étude est galiléen.


Il faut projeter cette relation vectorielle sur l'axe (Ox) et le tour est joué ...

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 12:52

Je vous rassure, les fiches que vous m'avez fourni ont été lu et comprise, j'essaie donc de les appliquer.
Le problème étant que je ne comprend pas, il est marqué sur votre fiche "Une action mécanique peut être modélisée par une grandeur physique appelée force et que l'on représente par un vecteur."
Donc la force électrostatique modélise bien l'action mécanique sur le proton, si non qu'en est il ?
Merci de vos réponses complètes et rapides

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 12:59

Pour la question 2, il nous manque pour calculer \Deltav et ainsi faire usage de la formule, la valeur de la vitesse finale (vf), et je ne vois pas comment la calculer, car ce qu'on cherche est \Deltat.

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 13:06

Raph26350 @ 18-03-2020 à 12:52

Je vous rassure, les fiches que vous m'avez fourni ont été lu et comprise, j'essaie donc de les appliquer.
Le problème étant que je ne comprend pas, il est marqué sur votre fiche "Une action mécanique peut être modélisée par une grandeur physique appelée force et que l'on représente par un vecteur."
Donc la force électrostatique modélise bien l'action mécanique sur le proton, si non qu'en est il ?
Merci de vos réponses complètes et rapides


Attention, j'ai juste voulu corriger le nom que tu donnais à \vec{F_e}, c'est effectivement une action mécanique sur le proton

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 13:07

Raph26350 @ 18-03-2020 à 12:59

Pour la question 2, il nous manque pour calculer \Deltav et ainsi faire usage de la formule, la valeur de la vitesse finale (vf), et je ne vois pas comment la calculer, car ce qu'on cherche est \Deltat.


Déjà, as-tu appliqué la deuxième loi de Newton ?

Donne-moi d'abord une relation vectorielle puis projette-là sur l'axe (Ox) pour la simplifier

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 19:24

dans un premier temps, la relation de la deuxième loi de Newton est Fe  ⃗m\frac{\Delta v}{\Delta t}
v varie t il ?, il me semble que oui car d'après le schéma la vitesse augmente (le vecteur vitesse est plus grand), comment déterminer \Delta v dans ce cas ?

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 19:40

Tu mélanges de nouveau les vecteurs et les valeurs ...

D'après la deuxième loi de Newton :

\sum \overrightarrow{F} \approx m \dfrac{\Delta\overrightarrow{v}}{ \Delta t} \\ \\ \Leftrightarrow \overrightarrow{P} + \overrightarrow{F_e} \approx m \dfrac{\Delta\overrightarrow{v}}{ \Delta t}

On a vu que le poids du proton est négligeable devant la force électrostatique appliquée à ce dernier :

\Rightarrow \overrightarrow{F_e} \approx m \dfrac{\Delta\overrightarrow{v}}{ \Delta t} \\ \\ \Leftrightarrow e \times \overrightarrow{E} \approx m \dfrac{\Delta\overrightarrow{v}}{ \Delta t}

On projette la relation suivant l'axe (Ox) :

e \times E \approx m \dfrac{\Delta v}{ \Delta t} \\ \\ \Leftrightarrow \boxed{e \times E \approx m \dfrac{v_f - v_0}{ \Delta t}}

Tu en déduis \Delta t = ?

Rappel : v_f = 4 \times v_0 d'après l'énoncé

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 19:51

Avant tout merci encore une fois de votre patience et surtout de votre rapidité.
Je viens de comprendre que l'on demande en effet l'expression littérale et non les valeurs, la moitié de la réponse est dans la question...
Je pense donc que \Delta t=\frac{m(vf-v0)}{e*E}
est-ce bien cela ?

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 19:57

Oui !

Et comme l'énoncé précise que v_f = 4 \times v_0 ...

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 20:19

Justement je ne sais pas si il faut le prendre en compte sachant que c'est écrit à la question 3 et pas avant

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 20:20

Il faut justement faire ceci à la question trois donc ?

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 20:26

Ton message du 18-03-20 à 19:51 répond à la question 2

Ensuite, même si je ne l'ai pas précisé, on a attaqué la question 3

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 20:36

D'accord, merci beaucoup, je vais essayer de faire cela, et vous montrer si tout convient bien

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 18-03-20 à 20:38

ça roule !

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 18-03-20 à 21:49

Voilà donc pour moi, \Delta t=\frac{m(4*v0-v0)}{e*E}
\Leftrightarrow \Delta t=\frac{1,7.10^{-27}(4*4,0.10^3-4,0.10^3)}{4,0.10^-16}
\Leftrightarrow \Delta t=\frac{2,04.10^{-23}}{4,0.10^-16}
\Leftrightarrow \Delta t=5,1.10^{-8} s
c'est donc le résultat en seconde attendu, est-il correct ?

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 19-03-20 à 09:10

Oui TB !

Tu peux le convertir en µs, ce sera plus parlant

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 19-03-20 à 10:43

Parfait dans ce cas, merci beaucoup, cela fait donc 5,1.10^{-2} \mu s

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 19-03-20 à 11:00

Ou on peut aussi dire que ça fait 51 ns ce qui est une très petite durée !

On a donc fini cet exercice.

Je te conseille de télécharger toutes les fiches de seconde et première fournies pour bien apprendre toutes les notions abordées par coeur, c'est primordial pour la mécanique.

Posté par
Raph26350re : Mouvements d'un système, accélération d'un proton 19-03-20 à 11:10

D'accord, merci beaucoup encore une fois, je pense que ces fiches pourront m'aider pour mon examen de spécialité que j'arrête en fin d'année.
Bonne continuation

Posté par
gbm Webmasterre : Mouvements d'un système, accélération d'un proton 19-03-20 à 11:34

Mais non il faut pas arrêter la physique-chimie, c'est génial !

Je t'en prie, à une prochaine fois peut-être, n'hésite pas à regarder les fiches disponibles et à reposer des question au besoin.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !