Inscription / Connexion Nouveau Sujet
Mouvements curviligne
Bonjour,
Voici l'énoncé: Une nageuse traverse une piscine à la nage dans une direction faisant un angle de 30° par rapport au bord de la piscine. Sa vitesse est de 2m/s. Calculer les composantes du vecteur vitesse dans la direction de:
a) la largeur
b) la longueur
Je fais un blocage complet, alors que ça parait si simple, pourriez vous me donner la formule, ou du moins une piste ...
Merci d'avance.
Bonjour,
En physique la vitesse est représentée par un vecteur  .
.
Ensuite, tu utilises ce que tu as appris en seconde sur les vecteurs...
Une base constituée de deux vecteurs ( et
et  ) de norme unité et orthogonaux (l'un parallèle à la largeur de la piscine, l'autre parallèle à sa longueur ; on suppose que le bassin est rectangulaire...)
) de norme unité et orthogonaux (l'un parallèle à la largeur de la piscine, l'autre parallèle à sa longueur ; on suppose que le bassin est rectangulaire...)
Un repère constitué d'un point O de la piscine (un angle par exemple) et de cette base. Ce repère (O ;  ,
,  ) sera donc orthonormé.
) sera donc orthonormé.
Le vecteur vitesse a dans ce repère des coordonnées x et y telles que  = x
= x + y
+ y
Les composantes de ce vecteur sont donc les deux vecteurs x et y
et y

Tout d'abord merci de me répondre si vite Coll 
Mais malgré ce que vous me dites, je ne vois toujours pas comment calculer les vecteurs :s
Les données que nous avons sont la vitesse et l'angle, j'ai bien saisi ce que sont les composantes, mais comment calculer leur valeur?
Merci 
J'espère que ça ne compte pas comme un double post :s
J'ai fait à tout hasard pour la largeur 2*sin(30) qui est égal à 1m/s et pour la longueur 2*cos(30) qui est égal à 1,7 m/s par chance se sont les bonnes réponses (j'ai les réponses à la fin du livre).
Mais faire cela sans rien comprendre ne m'intéresse pas, pouvez vous me donner une explication?
Merci encore
Le multi-post consiste à créer plusieurs topics pour le même problème.
Ceci n'a donc rien à voir avec le multi-post. Dans un topic que tu as créé, aussi longtemps que tu traites du problème initial, tu as le droit de poster autant de messages que tu veux !
_____________________
Un dessin :
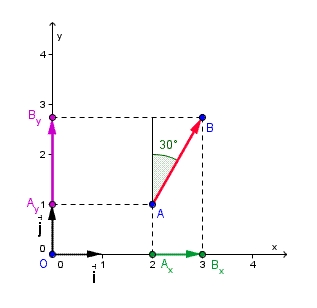
représente le vecteur vitesse. Sa norme vaut
. L'angle entre ce vecteur et le bord de la piscine vaut 30°
Un repère est créé. Origine : le point O. Base : les vecteurs  et
et  , vecteurs unitaires, parallèles aux bords de la piscine et donc orthogonaux. Le repère est ainsi orthonormé.
, vecteurs unitaires, parallèles aux bords de la piscine et donc orthogonaux. Le repère est ainsi orthonormé.
Sur l'axe Ox (dont le vecteur unitaire est  ) le vecteur
) le vecteur est projeté selon le vecteur
qui est la composante du vecteur
selon cet axe.
La norme de cette composante vaut
Sur l'axe Oy (dont le vecteur unitaire est  ) le vecteur
) le vecteur est projeté selon le vecteur
qui est la composante du vecteur
selon cet axe.
La norme de cette composante vaut

Merci beaucoup Coll 
Si j'ai bien compris l'utilisation soit du cosinus soit du sinus se fait par rapport à la projection du vecteur AB sur les axes i et j
Encore un énorme merci =)


