Inscription / Connexion Nouveau Sujet
Mouvement rectiligne varié
SVP aider moi à trouver ce problème physique
Deux voitures X et Y roulent dans le même sens,dans le même couloir sur une autoroute rectiligne. Elles roulent toutes deux à 108km/h, la distance qui les sépare étant de 50m. La voiture X se trouve devant Y.
A t=0 ,le chauffeur de la voiture X freine.
L'accélération de son mouvement est alors constante égale en valeur absolue à 3,80m/s².
Le chauffeur de la voiture Y, un peu distrait ne freine que 2secondes plus tard .son accélération est la même que celle de X.
1/Écrits la loi horaire du mouvement de la voiture X.
L'origine des espaces est la position de X à t=0.
2/Donnes la loi horaire du mouvement de Y.
3/Trouves la durée du freinage de x.
4/Montrer que la voiture Y restant dans le même couloir ne peut éviter de heurter la voiture x.
5/Trouves alors la vitesse chaque voiture au moment où le choc se produit.
D'accord voici la solution que je propose :
1/ l'équation horaire de la voiture X
a=cste --->MRUD
x=0,5(-3,8)t²+30t
x=-1,9t²+30t
2/ l'équation horaire de la voiture Y
*MRU
x=v0(t-t0)
x=30(t-2)-50
x=30t-110
*MRUD
x=1/2 a(t-t0)²+v0(t-t0)+x0
=-1,9(t-2)²+30(t-2)-50
3/calcul de la durée de freinage de de la voiture X
Vx=dx/dt=-3,8t+30
Si la voiture X freine sa vitesse s'annule
D'où -3,8t+30=0 ----> t=7,89 s
Question 1 :
Tu trouves x(X) = -1,9t² + 30t
OK
Question 2 :
Phase 1 : MRU entre les dates 0 et 2s
Tu trouves x1(Y) = 30t - 110
Impossible !
Ton équation donne x1(Y) = -110 m à la date t=0 ce qui est en contradiction avec l'énoncé.
Phase 2 : MRUD pour t>=2s
Tu trouves x2(Y) = - 1,9(t-2)² + 30(t-2) -50
Impossible !
Ton équation donne x2(Y) = - 50m à la date t=2s qui est en contradiction avec l'énoncé.
Pour la voiture Y (MRU)
L'équation horaire est de la forme x1(Y) = V0t + x0 et pas de la forme x=v0(t-t0) comme tu l'as écrit.
Pour la voiture Y (MRUD)
Tu as trouvé : x2(Y) = - 1,9(t-2)² + 30(t-2) -50 qui est la somme de trois termes.
Les deux premiers termes sont exacts mais pas le dernier.
Si la "durée" dont tu parles est celle du freinage de X alors oui est exacte si on admet que le freinage est resté inchangé après le choc.
Sinon le freinage prend fin à la date du choc ( la différence est faible).
Ci-dessous un graphique pour t'aider à vérifier tes résultats.
(Sauf erreurs .... )
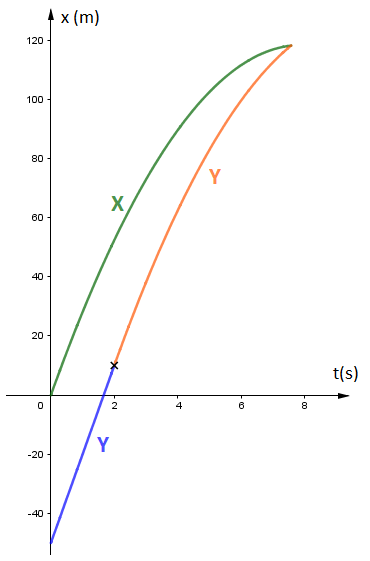
Résoudre les questions 4 et 5 nécessite d'avoir auparavant trouvé les résultats de la question 1 ( c'est fait ) et de la question 2 ( ce n'est pas fait )
Oui, c'est exact.
Le choc est inévitable s'il existe une date t=
inférieure à la durée de freinage de X telle que tu l'as calculée (7,89s) et pour laquelle x(X) = x(Y) (phase décélérée de Y)
Une fois cette date trouvée, il sera simple de calculer les vitesses de chacun des deux véhicules à cette date.
Annuler
connectez vous