Inscription / Connexion Nouveau Sujet
mouvement du centre d inertie d un solide
Bonsoir
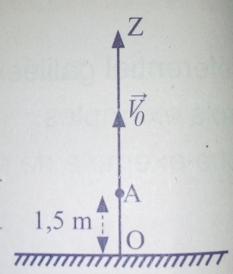
Déterminer par rapport au sol , la hauteur atteinte par le centre d inertie d une boule lancée avec la vitesse VO de valeur VO=4m/s
A partir du point A. g=9,8 m/s^2
Système : la boule
Referentief terrestre suppose galiléen
inventaires des forces
Le poids
Appliquons le théorème du centre d inertie
Vecteur P=ma
m*g*h=m*a
a=g*h
J n arrive pas introduire la vitesse VO dans l expression
Bonsoir,
Je te conseille d'appliquer le théorème de l'énergie cinétique, plus efficace ici que celui du centre d'inertie ( que tu appliques d'ailleurs de travers ! )
Je suppose, vu la figure, que la boule est lancée depuis le point A
On applique le théorème de l'énergie cinétique entre le point A de lancement pour lequel tu connais la vitesse v(A) et le point (S) ou la hauteur maximale est atteinte pour lequel tu connais la vitesse v(S)
Avant de commencer demande toi :
v(A) = ..........
v(S) = ...........
Appliquons le théorème de l énergie cinétique
ECs-EcA=mgh
1/2 m Vs^2=mgh
h=v^2/2*g
h=8/2*9,8
h=5,41 m
Ta as commis (au moins) 5 erreurs :
a) Tu as inversé les valeurs des vitesses.
La boule est lancée du point A avec une vitesse de 4m/s donc V(A)=4m/s
Elle s'arrête au point S donc V(S) = 0m/s
b) Si h représente la distance AS, le travail du poids est égal à - mgh . Il est négatif car il s'agit d'un travail résistant
c) Le carré de 4 n'est pas égal à 8
d) 8/(2*9,8) n'est pas égal à 5,41
e) La question demande de calculer la hauteur atteinte par rapport au sol. Ce n'est pas ce que tu as fait.
Bonsoir
La hauteur entre AS
On a
ECs-ECA=-mgh
-1/2 mVA^2=-mgh
h=VA^2/2*g
h=16/19,6
h=0,82 m
La hauteur par rapport au sol est
H=h(AO)+h(AS)
H=1,5+0,82
H=2,32 m


