Inscription / Connexion Nouveau Sujet
Mouvement des particules
Salut,
J'ai besoin de votre aide pour traiter mon exercice dont l'énoncé est:
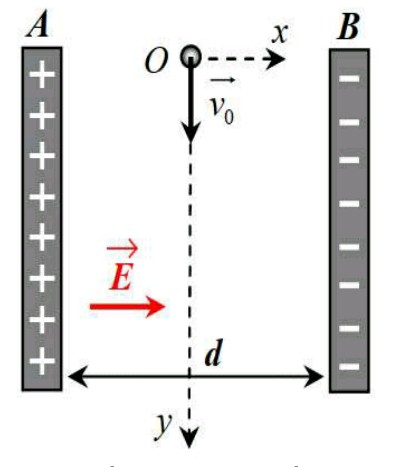
Un électron pénètre à t=0 en O, milieu de AB , dans un condensateur formé de deux armatures planes séparées de d=2,0 cm avec une vitesse initiale verticale Vo=50 km/s. Le référentiel du condensateur est galiléen. On négligera le poids des particules dans tout l'exercice.
2-1-1) Déterminer la tension entre les armatures A et B.
2-1-2) Exprimer le vecteur force électrique s'exerçant sur l'électron en fonction du vecteur champ électrique et de la charge élémentaire.
2-2) Définir le mouvement qu'aurait eu un neutron lancé en O à la même vitesse dans ce condensateur. Justifier rigoureusement.
2-3) Déterminer les coordonnées du vecteur accélération de l'électron dans le condensateur.
2-4) Déterminer l'équation cartésienne de la trajectoire de l'électron dans le condensateur puis préciser sa nature.
2-5-1) Sachant que les deux plaques mesurent D=5,0 cm de long, montrer que l'électron arrive à sortir du condensateur.
2-5-2) Déterminer la valeur de sa vitesse à la sortie du condensateur.
Données: masse électron m=9,1*10^(-31) kg; charge élémentaire e=1,6*10^(-19) C; champ électrique E=0,1 V/m.
Mon début:
2.1.1) Tension entre A et B:
on a E=U/d => U=E*d <=> U=0,1*0,02=0,002 V.
2.1.2) Expression du vecteur force électrique : j'ai écris -e parceque l'électron a une charge négative (?).
2.2) Sachant qu'un neutron ne renferme pas de charge, il aura un mouvement rectiligne uniforme suivant l'axe (Oy).
2.3) Coordonnées du vecteur accélération_
Application du théorème du centre d'inertie : <=>
. L'accélération est présente sur l'axe (Ox) mais pas sur l'axe (Oy).
Donc .
2.4) Équation cartésienne de l'électron dans le condensateur
En intégrant l'accélération par rapport au temps, on trouve la vitesse:
Vx=-eE/m (t)
Vy=Vo
En l'intégrant aussi, j'obtiens les équations horaires:
x(t)=(-eE/2m)t²
y(t)=Vo(t)
J'obtiens donc l'équation de la trajectoire : x=(-eE)/(2m*Vo²)y²
Cette trajectoire est une parabole.
2.5.1) Je montre que l'électron arrivera à sortir du condensateur:
Je ne sais pas quelle piste emprunter ...
Bonjour,
211) la formule c'est bonne, mais es-tu sûr de la valeur de E qui paraît tres faible ?
212)oui
2.2) oui mais il manque la justification rigoureuse
2.3) il faut écrire: (-Ee/m, 0) dans (O,x,y)
2.4) il faut expliquer pourquoi les constantes d'intégration sont nulles !
Et il faut écrire: y(t) = Vo.t
2.5.1) il faut trouver la position de l'electron en sortie donc quand y vaut ....
Et vérifier alors que x ne dépasse pas ...
*la valeur de E est vraiment faible: c'est ce que l'énoncé fourni.
2.2) la charge étant nulle, l'électron n'est ni attirée par la plaque A, ni par la plaque B. Initialement mis en mouvement avec la vitesse Vo (verticale) et orienté suivant (Oy), l'électron va, d'après la première loi de Newton garder son mouvement rectiligne uniforme suivant (Oy).
2.4) En integrant l'accélération, j'obtiens deux constantes ( Vo) suivant les deux axes. Mais la vitesse Vo est nulle suivant l'axe (Ox). L'intégration suivante fait apparaitre des constantes Xo et Yo, indiquant la position du début du mouvement ; le schéma montre que l'électron est l'origine du repère d'où Xo=Yo=0.
2-5-1) Lorsque y=D=0,05 m, x≈-0,009 m =-0,9 cm. x ne dépasse pas la distance d.
2.2) le principe d'inertie ne s'applique que si la resultante des forces est nulle. Il ne suffit pas ici de dire que la force électrique est nulle. Il faut aussi préciser que ...
2.4) oui
2.5) attention! ce n'est pas d la limite
2.2) le principe d'inertie ne s'applique que si la resultante des forces est nulle. Il ne suffit pas ici de dire que la force électrique est nulle. Il faut aussi préciser que ...
le poids est négligé
2.4) oui
2.5) attention! ce n'est pas d la limite
la distance D, longueur des armatures?
2.2) oui, le neutron n'est pas soumis à la force de Coulomb car sa charge est nulle, et son poids est négligé, donc il n'est soumis à aucune force et d'après le principe d'inertie, ... ...
2.5) non plus. Quelle est l'abscisse du point de l'armature A en sortie (donc " en bas" , en y=D )
Oui, et même -d/2< x < d/2
dans le cas général
Donc comme tu as trouvé en sortie xparticule = -0,9 cm
....
....
2.5.1)'à la sortie, l'électron est caractérisé par le point S (-d/2; D) . puis-je remplacer ces coordonnées dans l'équation de la trajectoire pour avoir Vo; la vitesse à la sortie?
2.5.2) attention! L'abscisse de S n'est pas -d/2
Et on demande la vitesse en S, pas la vitesse initiale Vo qui est connue.
précédemment,
Vx=-eE/m (t) (i)
Vy=Vo (ii)
x(t)=(-eE/2m)t² (iii)
y(t)=Vo*t (iv)
De (iv), t=y/Vo en remplaçant t dans (i), Vx=-eEy/mVo et (ii) : Vy=Vo
connaissant dont les coordonnées de V, puis je appliquer pour y=D la norme de V:
V=√(Vx²+Vy²) ?
Oui, c'est ca,
Si on appelle tS l'instant de passage en S (-0,9 cm, D) on a:
y(t) = Vo t => en S: D = Vo tS => ts = D/Vo
On en déduit la vitesse en S:
Vx= -eE/m . ts = -eED/(mVo)
Vy=Vo
Donc la valeur de la vitesse en S est: VS=√(Vx²+Vy²) = ....

 !
!

