Inscription / Connexion Nouveau Sujet
Mouvement des particules
Bonjour,
J'aimerais que vous m'aidiez à traiter mon exercice dont l'énoncé est le suivant :
Des particules de masse pénètrent dans une région où règnent un champ magnétique
et un champ électrique
uniforme et orthogonaux entre eux et à la vitesse
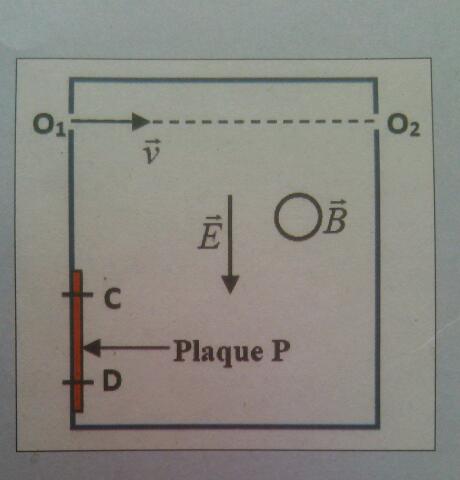
des particules à l'entrée O1 de la région comme l'indique la figure ci-contre. On constate que certaines des particules ont une trajectoire rectiligne horizontale et sont recueillies en O2 appartenant à la droite (O1
). Ces particules sont dites sélectionnées. On négligera leur poids devant les autres forces.
On donne: q=3,20*10^(-9) C; B=9*10^(-3) T; E=5*10^3 V/m.
1. Donner en justifiant la réponse, le sens du vecteur champ magnétique .
2.Montrer que la valeur Vo de la vitesse des particules sélectionnées ne dépend ni de la masse des particules, ni de leur charge électrique. Puis calculer sa valeur numérique.
3. On supprime le champ électrique. Les particules viennent alors heurter une plaque P placée verticalement dans la région (voir la figure). La mésure de l'écart entre les points d'impact extrêmes des particules sur la plaque donne CD=30,000mm.
3-1) Donner la nature du mouvement des particules dans la région puis donner l'expression de la grandeur caractéristique de leur trajectoire.
3-2)Calculer les valeurs Vmax et Vmin respectivement de la vitesse maximale et de la vitesse minimale des particules en admettant que la valeur Vo de la vitesse des particules sélectionnées est leur moyenne (Vo=(Vmin+Vmax)/2).
Mon début:
1) Le sens du vecteur champ magnétique dépend de celui de V et du signe q des particules; F=qE (q>0) et F=qV/\B : Donc V , B et F forment un trièdre direct, avec F (force de Lorentz ) ayant la direction de E.
De ce fait, Le champ B est sortant par rapport au plan de la figure.
2) En appliquant le théorème de l'énergie cinétique on a:
½mV²-½mVo²=W(F)
Avec F=qVB.
Ainsi, ½mV²-½mVo²=0 car F à la direction de E (perpendiculaire au déplacement ) dont son travail est nul.
Je trouve ainsi V=Vo...
Mais je doute 
Bonjour
De ce fait, Le champ B est sortant par rapport au plan de la figure.
Si pour toi, "sortant", signifie : orienté vers l'arrière de la figure, tu as raison.
Pour la question 2, tu montres que le champ magnétique ne peut pas modifier la norme du vecteur vitesse. Il s'agit plutôt d'établir la relation faisant intervenir force électrique et force magnétique pour que la particule garde une trajectoire rectiligne entre O1 et O2.
Bonjour
De ce fait, Le champ B est sortant par rapport au plan de la figure.
Sortant signifiait pour moi : orienté vers l'avant de la figure...je comprends pourquoi ça doit être orienté vers l'arrière...
Bonjour
De ce fait, Le champ B est sortant par rapport au plan de la figure.
Sortant signifiait pour moi : orienté vers l'avant de la figure...je comprends pas pourquoi ça doit être orienté vers l'arrière...
Pour que la particule garde une trajectoire rectiligne la force électrique doit être compensée par la force magnétique
donc :
Ok je vois...
2) Les deux forces se compensant,compensant, En norme on a la relation : Vo*B*sin(a)=E
a étant l'angle entre le vecteur vitesse et le vecteur champ magnétique (a=90°)
<=> Vo=E/B
Bonjour,
Il y a quelque chose qui me tracasse pour la question 1 :
Si les charges sont positives et si le champ magnétique est dirigé vers l'arrière alors la force magnétique au point O1 doit être verticale et dirigée vers le haut.
Mais alors quand on supprime le champ électrique (question 3) on ne voit pas trop comment les particules pourraient terminer leur course sur la plaque P
Autre cause de tracas : La valeur de la charge donnée par l'énoncé me semble irréaliste.
Bonsoir à tous
D'accord avec les remarques de odbugt1.
On peut imaginer de traiter le problème avec q=-3,2.10-19C
Autre possibilité : inverser le sens du vecteur E et choisir q=3,2.10-19C... Sans doute un peu plus réaliste compte tenu de la valeur de la masse de la particule.
Inverser le sens du vecteur E conduit aussi à inverser le sens du vecteur B. Ainsi, en présence du seul champ magnétique, les ions hélium vont être déviés vers la plaque
2) Les deux forces se compensant,compensant, En norme on a la relation : Vo*B*sin(a)=E
a étant l'angle entre le vecteur vitesse et le vecteur champ magnétique (a=90°)
<=> Vo=E/B
D'accord bien saisi

Cette expression de Vo est-elle valable?
Effectivement : seule les particules chargées de vitesse Vo=E/B ont un mouvement rectiligne entre O1 et O2.
Bonsoir
2)Sa valeur numérique est donc Uo = 5,56 x 10^6 mètres par seconde.
3-1) le mouvement des particules dans la région où regne le champ magnétique est circulaire et uniforme. la grandeur caractéristique de leur trajectoire est le rayon de courbure. D'après le TCI, F+P=ma (en vecteur). l'acceleration est normale . Suivant le sens de la force F de Lorentz, je trouve: F=ma=eVB , de plus a=V²/R où R est ce rayon de courbure.
=> R=Vm/eB.
3-2) Puis je appliquer le theoreme de l'é'ergie cinétique ici ?
Erreur sur la puissance de dix dans ton calcul.
3.1 : tu reprends sans doute un résultat de ton cours sans l'adapter exactement à la situation. Ici la charge de la particule  n'est pas égale à "e" mais vaut q=2e si on modifie l'énoncé conformément à mon message du 24-12-20 à 18:08.
n'est pas égale à "e" mais vaut q=2e si on modifie l'énoncé conformément à mon message du 24-12-20 à 18:08.
3.2 ; Le théorème de l'énergie cinétique ne conduit à rien d'intéressant ici. Il confirme juste le fait que le mouvement est uniforme : puisque une force magnétique de Lorentz ne travaille pas, l'énergie cinétique, donc aussi la norme du vecteur vitesse, restent constantes dans le champ magnétique.
Très simplement : appelons I le point d'impact des particules sur la plaque (I appartenant au segment CD) : quelle est la relation simple entre la distance (O1I) et le rayon R de la trajectoire ? Si cela ne te parait pas évident, complète la figure en y traçant la trajectoire de la particule entre O1 et I.
Très simplement : appelons I le point d'impact des particules sur la plaque (I appartenant au segment CD) : quelle est la relation simple entre la distance (O1I) et le rayon R de la trajectoire ? .
O1I est le diamètre du demi-cercle de rayon R formé.
=> R=O1I/2
C'est bien cela. En remplaçant R par l'expression obtenue précédemment, tu vas remarquer que C est le point d'impact des particules  de vitesse minimale et D le point d'impact des particules de vitesse maximale.
de vitesse minimale et D le point d'impact des particules de vitesse maximale.
R=V*m/q*B ; R=O1I/2
À partir de ces deux relations j'obtiens celle ci: V=(O1I*q*B)/(2*m)
-Pour I=C, on a une vitesse minimale
Vmin=(O1C*q*B)/(2*m) (i)
-Pour I=D, on a une vitesse maximale
Vmax=((O1C+CD)*q*B)/(2*m) (ii)
On sait que Vo=(Vmin+Vmax)/2; en substituant les relations (i) et (ii) dans cette relation, je trouve l'expression de O1C :
O1C=(4*Vo*m-CD*q*B)/(2*q*B)
En appliquant avec la valeur de q rectifiée , O1C=2,55m.
=> Vmin=5,52*10^5 m/s
=> Vmax=5,57*10^5 m/s


