Inscription / Connexion Nouveau Sujet
Mouvement de rotation autour de son centre d'inertie G.
Bonsoir à vous .
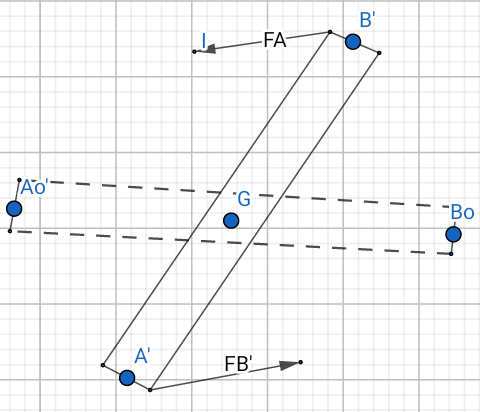
Une règle en plexiglas de longueur AB=50cm est mise en mouvement de rotation autour de son centre d'inertie G par un couple de forces ().
Le moment du couple est de 20 N.m et chaque force fait un angle beta =30° avec la direction de la règle.
Calcule l'intensité de FA et de FB .
Bonsoir,
Fais un schéma ( règle + forces )
Et applique ton cours ( Calcul du moment d'un couple de forces )
Ton schéma est très bien.
Il n'y a plus qu'à appliquer le cours sur le moment d'un couple de forces pour pouvoir répondre à la question posée.
Merci à vous voici ce que je trouve .
On a : Mc(FA;FB)= M∆(FA)+M∆(FB)
=FA×d+FB×d or MC(FA;FB)=20N.m
, FA=FB et d1 =d2 .
Donc Mc(FA;FB)=F×d
AN:
20=F×d ×cos(30°)
F=×0,86
F=34,4 N
Du coup FA=FB=34,4N
Non.
Que représente la distance "d" pour toi ?
Fais apparaître cette distance sur ton schéma.
Remarque : Ta méthode est correcte, mais lourde.
Il existe un moyen plus rapide pour calculer le moment d'un couple de forces que celui d'additionner les moments des forces qui constituent ce couple.
Remarque : Ta méthode est correcte, mais lourde.
Il existe un moyen plus rapide pour calculer le moment d'un couple de forces que celui d'additionner les moments des forces qui constituent ce couple. :
Oui j'ai hâte de connaitre votre méthode .
Le moment d'un couple de forces se calcule par la relation :
F représente l'intensité de l'une des forces, d est la distance qui sépare les directions des forces ( Voir schéma )
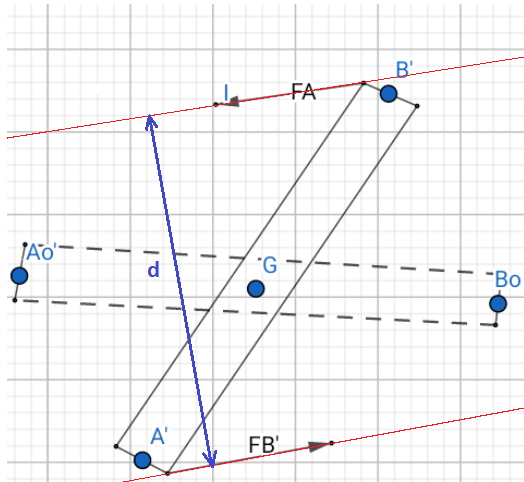
Donc Mc(FA,FB)= F ×d =F×ABsinβ
AN: 50cm=0,5m
Mc(FA;FB)=F×0,5×0,5
Or Mc(FA;FB)=20N.m
20=F×0,25
F=
F=0,0125N
Du coup F=FA=FB=0,0125N
Est ce juste ?
Donc Mc(FA,FB)= F ×d =F×ABsin(30°);
AN: 50cm=0,5m
Mc(FA;FB)=F×0,5×0,5
Or Mc(FA;FB)=20N.m
20=F×0,25
F=
F=0,0125N
Du coup F=FA=FB=0,0125N
Est ce juste ?
Ah oui une erreur de frappe
Donc 20 =F×0,25
F=
F=80N
F=FA=FB=80N
Merci à vous et aidez moi à faire l'autre exercice que j'ai posté il y'a 5 minutes s'il vous plaît.
Cette fois c'est exact.
D'autre part :
Je sais lire et si tu as posté un autre exercice je le verrai.
Inutile de me le signaler.