Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Mouvement de corps.

Posté par
kamikaz 29-12-20 à 19:17

Bonsoir ,

Merci d'avance.

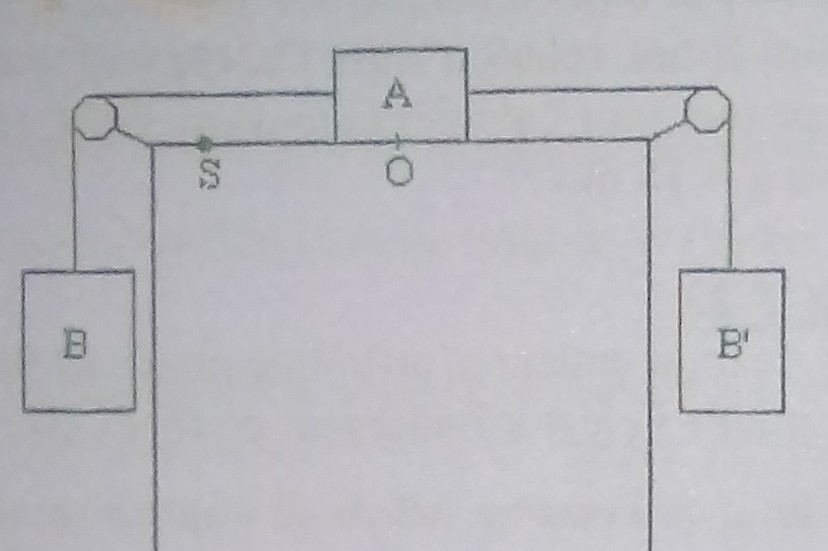
Un corps A de masse M= 1,66 g peut glisser sur une longue table horizontale. Comme l'indique le schéma ci-dessous.
Il est relié par des fils fins à deux autres corps : l'un B de masse M=0,490 kg et l'autre B' de masse m'=0,300 kg.
On suppose les masses des fils et des poulies négligeables ainsi que les frottements.

1) Calculer l'accélération du mouvement.

2) Calculer les tension T et T' des fils AB et AB'.

3) Quel est le temps mis par le corps A , partant de O , pour atteindre le point S à une distance OS= 2,189 m ?
Calculer sa vitesse en S.

4) Au moment où le corps passe en S , le fil casse brusquement. Décrire le mouvement ultérieure de l'ensemble des corps A et B'. Calculer le temps qui s'écoule entre le départ de A du point O et son retour au même point. On prendra g= 10 m/s².

Mouvement de corps.

Réponses

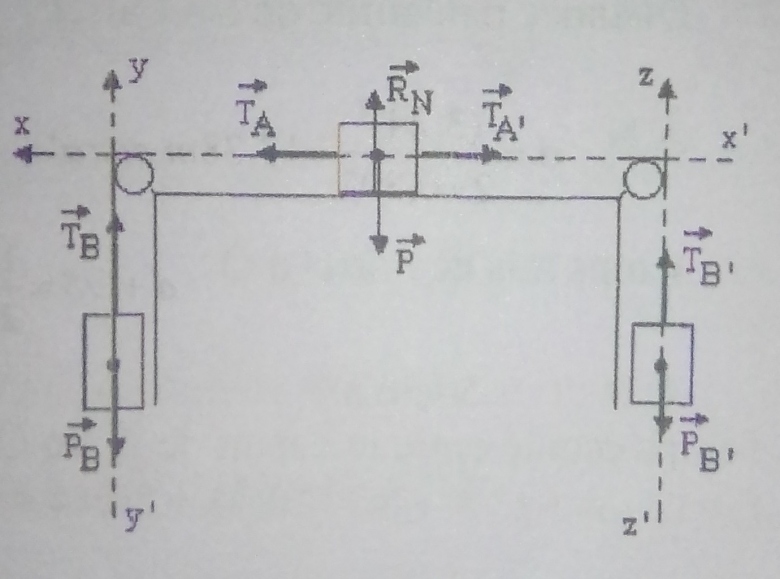
1) Mouvement de corps.

* Système : le corps A

Référentiel : Terrestre supposé galiléen.

Bilan des forces : \vec{R} , \vec{P} , \vec{T_{A}} et \vec{T'_{A}}.

Théorème du centre d'inertie :

\vec{R}+\vec{P}+\vec{T_{A}}+\vec{T'_{A}}=M\vec{a}

Dans la base (xy) , on a \vec{R}(0 ;R) ; \vec{P}(0 ;-P) ; \vec{T_{A}}(T_{A} ;0) et \vec{T'_{A}}(-T_{A} ;0) et \vec{a}(a;0)

Par projection sur (xx') ; on a :

T_{A}-T'_{A}=Ma

* Système : corps B

Référentiel : Terrestre supposé galiléen.

Bilan des forces : \vec{T_{B}} et \vec{P_{B}}

Théorème du centre d'inertie :

\vec{T_{B}}+\vec{P_{B}}=m\vec{a}_{B}

Dans la base (xy) , on a \vec{T_{B}}(0 ;T_{B}) ;\vec{P_{B}}(0 ;-P_{B}) et \vec{a_{B}}(0 ;-a_{B})

Par projection sur (y'y) , on a T_{B}-P_{B}=-ma_{B}

*Système : le corps B'.

Référentiel : Terrestre supposé galiléen.

Bilan des forces : \vec{T_{B'}} et \vec{P_{B'}}.

Théorème du centre d'inertie :

\vec{T_{B'}}+\vec{P_{B'}}=m'\vec{a}_{B'}

Dans la base (x'z) , on a \vec{T_{B'}}(0 ;T_{B'}) ; \vec{P_{B'}}(p ;-P_{B'}) et \vec{a}_{B'}(0 ; a_{B'}).

Par projection sur (z'z) , on a : T_{B'}-P_{B'}=m'a_{B'}

On a donc : T_{A}-T'_A=Ma

T_B-P_B=-ma_B

T_B'-P_B'=m'a_B'

Or T_A=T_B et T'_A=T_B'

T_B=-ma_B+P_B ; T_B'=m'a_B'+P_B'

Donc -ma_{B}+P_{B}-(m'{a_{B'}}+P_{B'})=Ma

==> -ma_{B}+mg-m'a_{B'}-m'g=Ma

Or a=aB=aB' car l'accélération est constante.

==>  -ma+mg-m'a-m'g=Ma

==> a(-m-m'-M)=m'g-mg

==> \boxed{a=\dfrac{m-m'}{m+m'+M}g}

Application numérique : m= 0,490 kg , m'=0,300 kg , M= 1,66.10-3 kg et g= 10 m/s².

a=2,4 m/s²

2) T= TB et T'=TB'

T=m(g-a) et T'=m'(a+g)

T= 3,72 N et T'= 3,72 N.

3) On a OS = 2,189 m

Donc OS=\dfrac{1}{2}at² ==> t=\sqrt{\dfrac{2×OS}{2,4}}

t=1,35 s

Par conséquent V_{S}=at=2,4×1,35=3,24m/s

V_{S}=3,24 m/s

4) * Mouvement ultérieure.

Système : corps A et B'.

Référentiel : Terrestre supposé galiléen.

Bilan des forces : \vec{P} , \vec{R} et \vec{P_{B'}}.

Théorème du centre d'inertie :

\vec{P}+\vec{R}+\vec{P_{B'}}=(M+m')\vec{a'}

Dans la base (xz) ; on a \vec{P}(0 ;-P) ; \vec{R}(0;R) et \vec{a'}(0 ;a')

==> -P+R-P_{B'}=(M+m')a'

P et R sont nuls car n'ont aucun effet ici.

D'où -P_{B'}=(M+m')a'

-m'g=(M+m')a'

a'=\dfrac{-mg}{M+m'} < 0

Donc \vec{a}.\vec{v}< 0.

Par conséquent le mouvement est rectiligne uniformément retardé..

*J'ai beau faire , je n'arrive pas à calculer le temps qui s'écoule entre le départ de A du point O et son retour au point O.

Posté par
vanoisere : Mouvement de corps. 29-12-20 à 19:24

Bonsoir
Je n'ai pas vérifié les applications numériques mais tout le reste est correct. Bravo !

Posté par
vanoisere : Mouvement de corps. 29-12-20 à 19:28

Pour le temps total : choisi une nouvelle origine de t au passage en S. Tu connais a, Vo et Xo.... facile alors d'obtenir la date de t positive correspond au passage en X=0. Il suffit alors d'ajouter cette durée à celle du mouvement de la première phase.

Posté par
kamikazre : Mouvement de corps. 30-12-20 à 10:20

Bonjour , je trouve 5 s' 16.

Et vous ?

Posté par
vanoisere : Mouvement de corps. 30-12-20 à 12:37

Je n'obtiens pas tout à fait ton résultat. Attention : une erreur que je n'avais pas remarquée dans mon précédent message : l'accélération a' fait intervenir m' au numérateur.
Remarque à propos de l'énoncé : il est incohérent de demander d'arrondir "g" à 10m/s2 tout en fournissant des données avec 3 ou 4 chiffres significatifs...

Posté par
kamikazre : Mouvement de corps. 30-12-20 à 15:43

Ok , mais vous trouvez combien pour le temps , parce que je ne trouve pas un autre résultat différent de 5s 16 ..

Posté par
kamikazre : Mouvement de corps. 31-12-20 à 15:14

Posté par
vanoisere : Mouvement de corps. 31-12-20 à 15:38

Quelle valeur de a' obtiens-tu ?

Posté par
kamikazre : Mouvement de corps. 31-12-20 à 15:52

a'= -0,302 m/s²

Posté par
vanoisere : Mouvement de corps. 31-12-20 à 19:00

avec m'=0,300kg et M=1,66kg, j'obtiens a'=-1,50m/s2
Vue le schéma, j'ai considéré comme irréaliste la masse M=1,66g fournie dans l'énoncé. Evidemment, cela amène à revoir aussi la valeur de a...
Même en prenant M=1,66g, je n'obtiens pas ta valeur de a'... J'obtiens a' peu différent de -g...

Posté par
kamikazre : Mouvement de corps. 01-01-21 à 18:38

Ah oui , mais faut que j'arrive à trouver ce temps écoulé..

Posté par
vanoisere : Mouvement de corps. 01-01-21 à 18:52

Pour cela, il faut être certain des valeurs de a et a'. Je t'ai expliqué que la valeur M=1,66g me semble peu réaliste ? Peux-tu vérifier ton document original ? Si tu tiens à faire les calculs avec M=1,66g, pourquoi pas : précise alors les valeurs de a et a'. Celle de a' que tu as fournie me semble fausse.

Posté par
odbugt1re : Mouvement de corps. 01-01-21 à 20:20

Bonsoir et bonne année vanoise et kamikaz
Si le lien suivant



fonctionne vous trouverez un fichier pdf comportant (c'est le dernier de la liste) un exercice, proche cousin de celui sur lequel planche kamikaz.
Comme pressenti par Vanoise, la masse du corps A y est de 1,66 kg

Posté par
vanoisere : Mouvement de corps. 01-01-21 à 22:46

Merci odbugt1 et meilleurs vœux pour cette nouvelle année !

Posté par
kamikazre : Mouvement de corps. 02-01-21 à 08:19

OK , merci et meilleures vœux à vous deux !

Pourriez vous me montrer le processus à suivre pour déterminer ce temps ?

Ensuite j'ai  fait l'exo 2 (physique) du fichier que vous avez envoyé mais je ne sais pas si mes réponses sont justes.

Posté par
kamikazre : Mouvement de corps. 02-01-21 à 18:24

Bonsoir

Posté par
vanoisere : Mouvement de corps. 02-01-21 à 19:39

Avec g=9,81m/s2 et M=1,66kg, l'accélération avent la coupure du fil est a=0,761m/s2. Avec xs=2,189m, on obtient :

t_{s}=\sqrt{\frac{2x_{s}}{a}}=2,40s\quad;\quad v_{s}=a.t_{s}=1,825s

On conservant les mêmes origines pour t et pour x, l'équation horaire du mouvement après la rupture du fil est :

x=\frac{1}{2}a'.\left(t-t_{s}\right)^{2}+v_{s}.\left(t-t_{s}\right)+x_{s}

La valeur de a' a déjà été calculée : a'=-1,50m/s2.

La durée totale du mouvement jusqu'au retour de A à sa position de départ x=0. Il s'agit donc de résoudre l'équation du second degré précédente. La durée recherchée est la valeur positive de t correspondant à x=0.

Posté par
kamikazre : Mouvement de corps. 03-01-21 à 08:28

Je vois , c'est du simple bon sens..

Merci


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !