Inscription / Connexion Nouveau Sujet
Mouvement dans un champ uniforme
Bonjour, bonnes fêtes 🥂 à vous !
Veuillez m'assister ici svp
Problème
Une piste verticale est constituée d'une partie circulaire AB et d'une partie horizontale BC tangentiellement raccordées. AB est un quart de cercle de rayon r = 32 cm et BC = L = 25 cm. En dessous de C, à la distance h = 15 cm, un plan horizontal coupe en D la verticale passant par C. Une petite sphère métallique (S) de masse m = 200 g, supposée ponctuelle est abandonnée en A sans vitesse initiale.
1) On néglige les frottements sur la piste ABC.
a) Calculer la vitesse de la sphère lors de son passage en B et en C.

Bonjour mon cher krinn !
1.a) vitesse de la sphère en B et en C
- système : sphère (S) de masse m ;
- référentiel : terrestre (supposé galiléen) ;
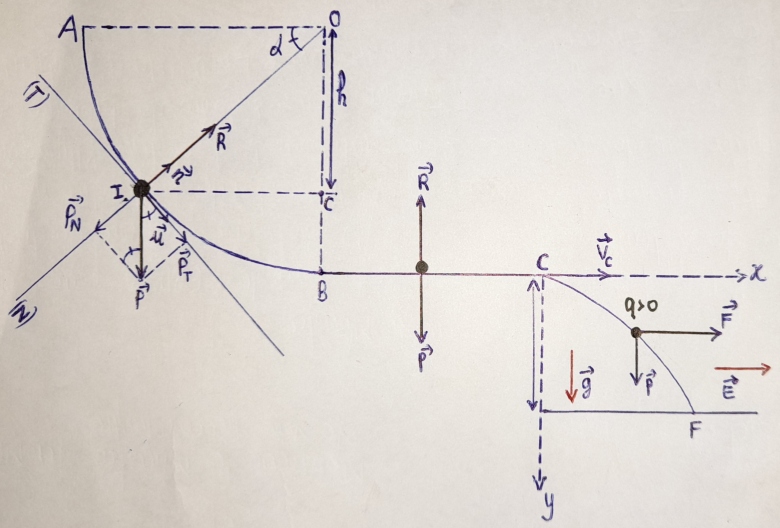
- bilan des forces : le poids de la sphère et la réaction
de la piste sur la sphère. (Figure)
Application du Théorème de l'énergie cinétique entre A et I :  Ec =
Ec =  W(
W()
Donc : ½mVI² - ½mVA² = W() + W(
)
Or VA = 0 ; W() = +mgh et W(
) = 0
Alors ½mVI² = mgh  VI² = 2gh
VI² = 2gh
Sur la figure, la hauteur de la chute du poids de A à I est : h = r.sin
Donc VI² = 2gr.sin
• En B,  = 90⁰, donc sin
= 90⁰, donc sin = 1
= 1
Alors =
D'où VB = 2,5 m/s
• En C, VC = VB puis que :
W() = 0, car
est normale et W(
) = 0 car B et C se trouvent au même niveau d'altitude.
Donc VC = 2,5 m/s
1.b) Réaction de la piste au point I
- système : sphère (S) de masse m ;
- référentiel : terrestre (supposé galiléen) ;
- bilan des forces : le poids de la sphère et la réaction
de la piste sur la sphère. (Figure)
Application du Théorème du centre d'inertie :
 (
() = m.

+
= m.
Dans la base de Frenet et suivant la normale , on a :
AN : m = 0,2 kg ; g = 9,8 N/kg ;  = 45⁰
= 45⁰
Je trouve R = 1,33 N
J'ai calculé R comme si l'expression était sous un radical, oups !
C'est risqué de faire la physique pendant les fêtes 
C'est bien R  4,2 N !
4,2 N !
Avant d'aborder la question suivante, quel est le code pour écrire l'arc AB en Latex ? C'est-à-dire mettre un arc sur AB.
Merci bien mon cher !
Question 2 : On demande de Calculer VB et VC en présence des forces de frottement.
- système : sphère (S) de masse m ;
- référentiel : terrestre (supposé galiléen) ;
- bilan des forces : le poids de la sphère et la réaction
de la piste sur la sphère. (Figure)
Application du Théorème de l'énergie cinétique entre A et B :  Ec =
Ec =  W(
W()
Donc : ½mVB² - ½mVA² = W() + W(
)
Or VA = 0 ; W() = +mgr et W(
) = - f.
Mais = r.
 /2
/2
Enfin, j'obtiens
AN : VB  2,18 m/s
2,18 m/s
Calculons VC : je fais la même chose, en appliquant le TEC entre B et C. Le travail du poids est nul, mais le travail de la réaction est : W() = - f.L
J'obtiens enfin Vc² = VB² - 2.f.L/m
AN : Vc = 2 m/s
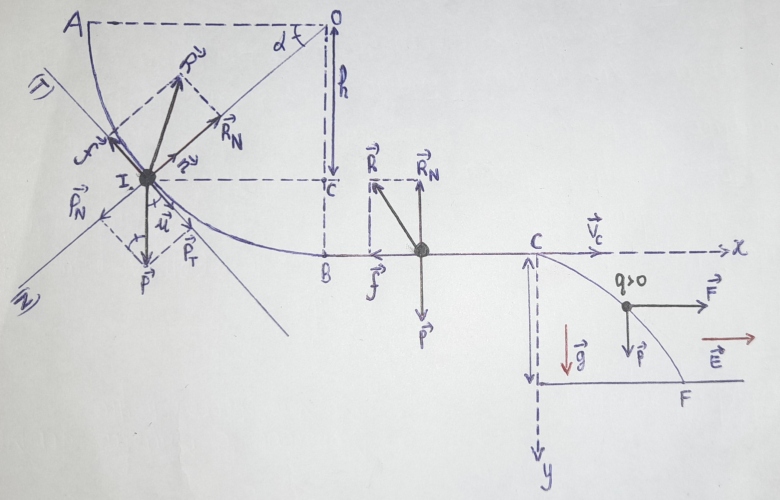
3.a) Bilan des forces appliquées sur la sphère :
- Le poids de la sphère ;
- la force électrique .
b) Montrons que la somme de ces forces est constante
Comme et
sont des vecteurs constants, alors la somme donne un vecteur constant.
Nature du mouvement : le mouvement de la sphère est plan. La trajectoire est contenue dans le plan (Cx, Cy)
c) Coordonnées de et de
Le Théorème du centre d'inertie donne :
• Le vecteur vitesse à l'instant t est :
En remplaçant par son expression, j'obtiens :
Dans le repère Cx, Cy les composantes du vecteur vitesse à l'instant t sont :
et
C'est-à-dire, j'ai projeté l'expression vectorielle du vecteur vitesse dans le repère Cx, Cy.
• Je fais la même chose pour le vecteur espace, qui est de la forme :
L'instant initial est la date où la sphère passe en C, donc x0 = 0 et y0 = 0
Je trouve les composantes du vecteur position dans le repère Cx, Cy par projection :
et
Ensuite j'élimine le temps t entre x et y pour trouver x = f(y). C'est ça ?
3b) si la somme des forces est constante, alors ...... est aussi un vecteur constant, donc le mvt est ....
3c) oui
A mon avis, il vaut mieux partir des equa. diff. :
x" = qE/m
y" = g
Et integrer 2 fois pour trouver x', y', puis x et y, en utilisant les conditions initiales.
3b) si la somme des forces est constante, alors
Oui, j'ai utilisé au brouillon la méthode des intégrales, j'ai trouvé la même chose. Moi je préfère utiliser la projection des expressions vectorielles sur un système d'axes puis en déduire les équations horaires. C'est très simple !
d) Coordonnées du point F
Le point F étant sur la trajectoire, ses coordonnées doivent vérifier l'équation de la trajectoire.
En F, yF = h = 15 cm et quand je remplace dans l'expression de x = f(y) je trouve xF = 38 cm.
Date d'arrivée en ce point
Je passe par l'équation horaire de y :
y = ½gt², or en F, y = 15 cm.
Je tire t puis je trouve : t = 0,17 seconde.
Mais ce temps là est trop petit pour moi, je ne suis pas sûr avoir trouvé la bonne réponse.
D'accord.
Vous dites 15 cm de chute libre. Est-ce qu'il s'agit réellement d'une chute libre, puisque la force électrique est aussi appliquée ?
Ce nest pas une chute libre, mais le temps de chute est le meme que si c'en etait une!
(y= 1/2 gt2)
La force electrique modifie ici la portée de la chute, mais pas  t (en comparaison de la chute libre si E est nul )
t (en comparaison de la chute libre si E est nul )


