Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Mouvement dans un champ électrostatique uniforme
Posté par Souriceau
Bonjour, j'ai une question par rapport à un exercice sur l'étude du mouvement d'un électron dans un champ électrostatique uniforme.
Voici l'énoncé :
Citation :
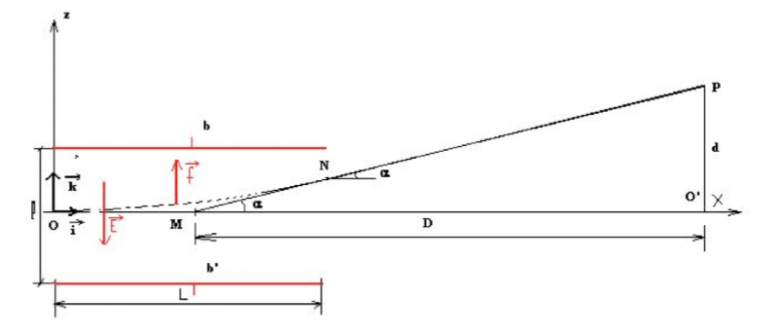
Un champ électrique règne entre deux plaques parallèles séparées d'une distance ℓ. Un électron de masse m et de charge électrique -e est émis au point O avec une vitesse initiale V0 dirigée selon le sens positif de l'axe des x. L'électron sort du dispositif au point N puis se déplace dans le vide en ligne droite de N vers P où il percute un écran à la distance d de l'axe des x.
Un champ électrique règne entre deux plaques parallèles séparées d'une distance ℓ. Un électron de masse m et de charge électrique -e est émis au point O avec une vitesse initiale V0 dirigée selon le sens positif de l'axe des x. L'électron sort du dispositif au point N puis se déplace dans le vide en ligne droite de N vers P où il percute un écran à la distance d de l'axe des x.
Voici le schéma avec l'énoncé : (voir image attachée)
Dans la première question on me demande de montrer que la trajectoire de l'électron est une parabole.
Donc j'applique la seconde loi de Newton. J'ai
Fext = m.a ; l'électron n'étant soumis qu'à la seule force électrostatique F=-eE, il vient :
F = m.a
-eE = m.a
d'où :
a = -eE/m
E et a étant de sens contraire, on obtient les coordonnées du vecteur accélération suivantes :
a (x(t) = 0 ; z(t) = eE/m)
Après des intégrations successives et compte tenu du fait que l'angle
du vecteur vitesse initiale v0 avec l'horizontale est nul, , on obtient les coordonnées du vecteur position OM suivantes :
OM (x(t) = v0.t ; z(t) = eE.t2/2m)
Finalement, on obtient l'équation cartésienne de la parabole :
z = eE.x2/2v02m
Seulement dans la correction, le résultat est différent. D'une part, voici ce qui est écrit pour les coordonnées du vecteur accélération :
Citation :
m.a = -eE donc m.d2z/dt2 = e.E et m.d2x/dt2 = 0. Cela donne donc comme équation : z(x) = 1/2.eE.x2/v02.
m.a = -eE donc m.d2z/dt2 = e.E et m.d2x/dt2 = 0. Cela donne donc comme équation : z(x) = 1/2.eE.x2/v02.
Je comprend l'écriture (c'est la dérivée seconde) cependant je ne comprend pas pourquoi la masse m a disparu de l'équation. J'ai pourtant revérifié mes calculs et comparé avec d'autres exercices.
Plus tard dans l'exercice, on demande d'établir l'angle
formé par le vecteur vitesse avec l'horizontale. Dans la correction, je suis censé obtenir :
Citation :
tan() = eEL/v02
tan(
) = eEL/v02Je n'arrive pas à établir cette relation.
Merci d'avance pour vos réponses !
Annuler
connectez vous