Inscription / Connexion Nouveau Sujet
mouvement dans un champ de pesanteur uniforme (physique)
Bonjour,
Voici un exercice que je n'arrive même pas a commencer en physique,
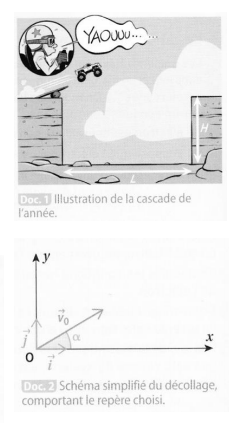
"Un homme veut effectuer la cascade de l'année en sautant par dessus le grand canyon aux usa. il connait les caractéristiques du canyon a l'endroit choisi (largeur= 1.25km et profondeur=1.7km) le tremplin fait un angle a=30° au dessus de l'horizontale. la voiture et son équipage seront modélisés par un point M de masse m=1230kg (autres forces que le poids négligées)
Le mvt est plan donc on ne considère que les coordonnées x et y du système
(donnée : g = 9.81 N.kg-1)
1) exprimer les coordonnées du vecteur vitesse initiale v0 dans le repère choisi
2) en utilisant la 2eme loi de newton dans le référentiel terrestre supposé galiléen déterminer l'accélération subie par le système
3) en déduire les équations horaires de la vitesse vx(t) et vy(t)
4) a partir de la question précédente montrer que les coordonnées x(t) et y(t) du système vérifient : x(t)=v0cos(a)t et y(t)=1/2gt2+v0sin(a)t
5) en supposant que le saut est réussi, déterminer l'expression de la durée du saut delta t saut puis celle de la distance horizontale D parcourue pendant le saut, en fonction de v0, a et g
6) quelle condition D doit elle vérifier pour que le saut soit réussi ? en déduire la valeur de la vitesse initiale v0 nécessaire a la réussite du saut, en km.h-1. calculer la durée du saut correspondante.
Voila, je vous remercie d'avance pour votre aide surement précieuse 
Bonjour,
Bienvenue sur le forum.
Avoir recopié entièrement son énoncé d'exercice c'est un début mais ce n'est pas suffisant :
Je te conseille de lire attentivement cette fiche de cours (clique sur la maison) :
Une fois que ce sera fait, tu seras en mesure de nous proposer tes pistes de réflexion pour initier un échange là-dessus.

ok du coup je viens de lire tt ca et pour moi ce serait:
1)v0 |v0x= v0cos(a)
|v0y= v0sin(a)
2) dapres la 2eme loi de newton, somme des forces ext = ma
P = ma
g = a
donc a = g = 9.81m.s-2 (je suis pas sure de l'unite la par contre :'))
3)vx(t)= v0cos(a) et vy(t) = gt+v0sin(a)
4)v=dOM/dt donc OM |x=v0cos(a) * t + cte
|y=1/2gt2 + v0sin(a) * t + cte (ici cte=0)
5) la je sais vrmt pas ...... je bloque bloque bloque sur cette question... merci de votre aide 
(Bien sur ne pas tenir compte des vecteurs etc mais je ne sais meme pas comment les mettre hihi)
++ jai oublie de vous mettre les illustrations / schemas dans le 1er post je les met de suite
Bon, il va falloir déjà régler une chose : le multi-compte est strictement interdit sur le forum  :
:
Merci donc de régulariser ta situation en supprimant ton compte Hannahcool.
Une fois que ce sera fait, contacte malou (
***Situation régularisée (21h29)***
Bonjour,
1. Attention à ne pas confondre vecteur et composante d'un vecteur dans un repère :
 extrait de
extrait de Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
OK sinon
2. Pour être en mesure d'écrire cela, il faut modéliser le problème en définissant le système étudié, le référentiel d'étude, faire un bilan des forces avec les hypothèses faites, avant d'appliquer la deuxième loi de Newton.
De même ici, on écrit d'abord une relation vectorielle avant de la projeter dans le repère d'étude.
Une intensité de la pesanteur est en N/kg ou en m/s²
3. Tu n'expliques pas ce que tu fais
4. Pourquoi cte = 0 ? Il faut expliquer ce que tu fais
5. Quelle équation déterminée pourrait nous aider à déterminer cela ?

ok mercii
(donc la 1 c'est pas bon ? ca jai pas compris...)
2) systeme : voiture et son équipage modélisés par un point M de masse m=1230kg
referentiel : terrestre supposé galiléen
bilan des forces : P=mg
(... jusqu a g=a=9.81m.s-2)
3)vx = cte 1 or cte 1 = v0cos(a) donc vx=v0cos(a)
vy=gt+ cte2 or cte 2 = v0sin(a) donc vy=gt+v0sin(a)
je suis pas tres sure d'avoir explique mais sur le schema vx n'a pas de coeff directeur (donc cte) et vy oui c'est donc g multiplié par la variable t
4)je refais la meme chose mais en expliquant que, a t=0s, OM0|x=0
|y=0
donc les constantes sont egales a 0
(et v=dOM/dt)
donc OM |x=v0cos(a) * t (->car la primitive d'une cte est 1 "fonction linéaire")
|y=1/2gt2 + v0sin(a) * t (-> "" + primitive de t est 1/2t2)
5)(je ne sais pas si c'est bon mais je pense que c'est) x=v0cos(a)*t -> t=x/v0cos(a)
je ne sais pas si elle est necessaire mais l'equation de la trajectoire est
y=-g/2 * x2/v0cos2(a) + tang(a)*x
ou d=v*t donc peut etre que ca a un rapport mais la je bloque totalement ?????
j'ai également une autre question par rapport à la q1, c'est quoi "le repère choisi", est ce que l'on doit préciser "repère orthonormé, cartésien ou autre" svp??
encore merci 
donc pour la 3 c'est
vx=v0cos(a)
vy=-gt+v0sin(a)
et la 4 : les equations verifient bien que x(t)=v0cos(a)t et y(t)=1/2gt2+v0sin(a)t
ok mercii
(donc la 1 c'est pas bon ? ca jai pas compris...)
Je te dis juste de bien respecter le formalisme d'un vecteur :
2) systeme : voiture et son équipage modélisés par un point M de masse m=1230kg ok
referentiel : terrestre supposé galiléen ok
bilan des forces : P=mg idem ici, commence par écrire tes expressions sous la forme vectorielle
(... jusqu a g=a=9.81m.s-2)
Pas d'accord sur le signe : si on applique la deuxième loi de Newton :
3)vx = cte 1 or cte 1 = v0cos(a) donc vx=v0cos(a)
vy=gt+ cte2 or cte 2 = v0sin(a) donc vy=gt+v0sin(a) erreur de signe sur l'expression, il semble que tu dois réviser la projection du vecteur accélération dans le repère d'étude (O,x,y)
je suis pas tres sure d'avoir explique mais sur le schema vx n'a pas de coeff directeur (donc cte) et vy oui c'est donc g multiplié par la variable t
4)je refais la meme chose mais en expliquant que, a t=0s, OM0|x=0 oui !
|y=0
donc les constantes sont egales a 0 ok
(et v=dOM/dt)
donc OM |x=v0cos(a) * t (->car la primitive d'une cte est 1 "fonction linéaire") ok
|y=1/2gt2 + v0sin(a) * t (-> "" + primitive de t est 1/2t2) de nouveau, erreur de signe, cf. la fiche fournie
5)(je ne sais pas si c'est bon mais je pense que c'est) x=v0cos(a)*t -> t=x/v0cos(a)
La solution est dans la fiche :
La portée de la balle est la distance séparant le point de départ de la balle et le point d'arrivée (D sur le dessin).
L'ordonnée au point de chute est nulle.
Comme
je ne sais pas si elle est necessaire mais l'equation de la trajectoire est
y=-g/2 * x2/v0cos2(a) + tang(a)*x
ou d=v*t donc peut etre que ca a un rapport mais la je bloque totalement ?????
Encore merci énormément 
Pour les questions 1 à 4 c est rectifié, merci!
Pour la 5, je crois avoir compris, donc ce serait d'abord trouver y=0 (donc le point d'arrivée), puis on divise par t (ca je ne suis pas sure de comprendre pourquoi) pour enfin trouver t grace a cette équation (ca c'est clair! ), c'est ca ? :')
), c'est ca ? :')
Ensuite, pour trouver D, il faudrait donc utiliser l'angle de 30° je suppose mais comment on fait svp ?
Ok pour les questions 1 à 4, tu avais fait une erreur de projection du vecteur champ de pesanteur sur l'axe (Oy).
Pour la question 5, effectivement, le saut est réussi dès que y(t) = 0 (on retouche le sol). On utilise donc les équations trouvées pour déterminer la durée correspondante.

Ok donc est ce que ce serait donc t = 2v0sin(a) / g et y(x)=-g/2 * x2/v0cos2(a) + tang(a)*x pour trouver le D ou je me trompe totalement ? (c'est fort possible haha on n'a jamais vu ca en cours je suis un peu perdue sur la méthode :3)..
merci encore 
As-tu lu ce que j'ai écrit dans mon message du 29-10-20 à 13:44 ?
Pour mémoire, tout est dans la fiche que je t'ai fournie : ![]() Mouvement d'un projectile dans le champ de pesanteur
Mouvement d'un projectile dans le champ de pesanteur
Idem pour la détermination de D = portée.

Ok ok du coup c'est tout ca :
"La portée de la balle est la distance séparant le point de départ de la balle et le point d'arrivée (D sur le dessin).
L'ordonnée au point de chute est nulle..
Comme t_p est non nulle alors on a :
On insère la valeur de t_p dans l'équation x(t).
Ce qui, simplifié, donne : "
(bref la fin de la fiche)
sans rien modifier ? (a part balle par voiture hihi)
dans ce cas merci beaucoup 
et je vous demandrais encore juste de m'aider svp pour la q6 , est ce quil faut dire si D doit etre compris entre différentes valeurs etc..?
merci merci merci en tout cas
***Latex ajouté***
C'est bien cette partie de la fiche qu'il faut adapter aux données de l'énoncé.
Pour la question 6, si le système tombe dans le trou c'est que le saut est un échec : il faut donc dépasser la longueur L du trou (condition min).
Et pour la condition max, c'est la définition de la portée calculée en question 5

Ok donc pour la q5 si j'ai bien compris le delta t saut vaut (2v0sin(a)) / g et la distance D (qui est donc le x dans l'équation) vaut (v0^2sin(2a)) / g -> soit t = (2v0sin(a)) / g et
D = (v0^2sin(2a)) / g | c'est ca ? 
Maintenant pour la 6, on doit dire que D = (v0^2sin(2a)) / g superieur à la largeur L=1.25km , donc je suppose que c'est une sorte d'inéquation (peut etre que je me trompe complétement mais j'aurais essayé hihi) :
(v0^2sin(2a)) / g 1.25
1.25
1.25 = sin (2*30) * v0^2 / 9.81
1.25 * 9.81 / sin (60) = v0^2
-40.2 = v0^2
 -40.2 et la c'est faux mais je pense que c'etait pas la bonne equation enfaite
-40.2 et la c'est faux mais je pense que c'etait pas la bonne equation enfaite
 vous pouvez encore une fois m'aider svp ?
vous pouvez encore une fois m'aider svp ?
5. Il faudrait que tu sois un peu plus convaincue de ce que tu écris :
* D est distance séparant le point de départ du système ( = 0s) et le point d'arrivée (que tu n'as qu'à noter
pour être plus cohérent avec l'exercice).
* alors la durée du saut est
6. Avant de dérouler des calculs, il faut raisonner physique : ton système aura réussi son saut dès lors que la portée est supérieure à la distance L.
Cela doit te permettre d'aboutir à une expression littérale de .
On verra après pour le calcul numérique, mais sin(60°) n'a jamais donné une valeur négative, il faut revoir ta trigonométrie ...
ah d'accord donc à la fin de la 5, on a quand meme:
t(D)= (2v0sin(a)) / g
D = (v0^2sin(2a)) / g
(raisonnement précédent)
6) Le système aura réussi son saut dès lors que la portée est supérieure à la distance L:
L  D
D
L (v0^2sin(2a)) / g
(v0^2sin(2a)) / g
L*g / sin(2a)  v0^2
v0^2
 L*g / sin(2a)
L*g / sin(2a) v0
v0
soit (calcul numérique)
 1.25*9.81/sin(60)
1.25*9.81/sin(60) v0
v0
14.16 v0
v0
la valeur de la vitesse initiale v0 nécessaire a la réussite du saut est donc 14.16km.h-1
t = d/v
= [(2v0sin(a)) / g] / 14.16
= (2*14.16*sin(30) / 9.81) / 14.16
= 0.10h = 6minutes
c'est ca ?? (ca m'a pas l'air trop faux en tout cas  )
)
Tes calculs sont à revoir ... Je te rappelle qu'on doit faire une application dans les unités SI :
- une distance convertie en m,
- une masse en kg,
- etc.
ok donc si je reprends mon ancienne réponse mais que je change les unités ca fait
"->":
q5, on a donc:
t(D)= (2v0sin(a)) / g
D = (v0^2sin(2a)) / g
6) Le système aura réussi son saut dès lors que la portée est supérieure à la distance L:
L  D
D
L (v0^2sin(2a)) / g
(v0^2sin(2a)) / g
L*g / sin(2a)  v0^2
v0^2
 L*g / sin(2a)
L*g / sin(2a) v0
v0
soit (calcul numérique)
 1.25.10^3*9.81/sin(60)
1.25.10^3*9.81/sin(60) v0
v0
119m.s-1 v0
v0
la valeur de la vitesse initiale v0 nécessaire a la réussite du saut est donc 119m.s-1, soit 428km.h-1 (bon bah je crois encore que c'est faux finalement)
t = d/v
= [(2v0sin(a)) / g] / 119
= (2*119*sin(30) / 9.81) / 119
= 0.9secondes
bon, c'est pas ca du coup :') mais je ne vois pas la ou j'ai encore faux au niveau des unités.....
merci de votre réponse 
5. OK
6. On cherche la condition sur la vitesse telle que la portée dépasse la largueur du canyon, soit
Application numérique :
soit
Ce qui est énorme je te l'accorde ... Après, faire traverser un objet de plus d'1 tonne sur 1,25 km ... Ou alors une coquille introduite quelque part ...
Concernant la durée, attention, tu n'est pas en vitesse linéaire, cette formule n'est donc pas correcte. Je te rappelle que tu as vu une expression en question 5 ...

ok parfait merci beaucoup pour la confirmation de la q5 et du debut de la q6,
pour la fin de la 6, est ce que :
On sait que t(D)= (2v0sin(a)) / g
donc t(D)= (2*119*sin(30)) / 9.81 = 12.13 secondes
est correct svp, ou faut il mettre v0 en km/h et le resultat en h ?
Merci de votre réponse 
Ton calcul m'a l'air correct.
Pour les conversions d'unité, pour ne pas te planter, reviens toujours dans les unités SI avant de conclure par celle demandée par l'énoncé


 moteur de recherche
moteur de recherche page de choix du forum
page de choix du forum fiches du site
fiches du site guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
