Hello,


As-tu avancé ?

Bonsoir,

Tes deux premières questions sont exactes (présentation de la question 2 toujours aussi détestable !)

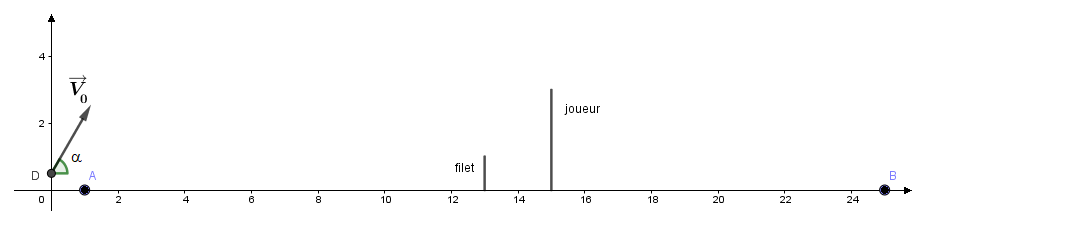
Ci dessous un schéma pour t'aider à démarrer la suite.
A et B sont les extrémités du terrain.
Le joueur est représenté bras levé.
D est le point de départ de la balle.
O est l'origine des espaces
est l'angle de départ de la balle.

Bonjour.
Il parait que les Équations sont les mêmes  que celle trouvé dans la question précédente

Je ne sais pas trop ce que tu désignes par "question précédente"

Question 2.2 :
L'équation de la trajectoire de la balle s'obtient en éliminant le temps entre les équations horaires déjà obtenues :

y=-g/2VO^2Cos^2(a)+xtan a+h

Question 3
Comment justifier ?

Question 2.2
Ton équation est peu lisible.
De plus il lui manque un terme.

L'équation correcte est :



Question 3 : Le joueur de la zone B ne pourra pas intercepter la balle si celle ci passe au dessus de l'extrémité de sa raquette avec une altitude supérieure ou égale à H
Dans le cas contraire, l'interception devient possible.

Question 4
Si la balle passe au dessus de l extrémité de sa raquette avec une altitude supérieure où égale a H.
Dans ce cas la balle retombe dans l aire de jeu

Question 3 :
Soit x_J  l'abscisse du joueur  
Pour savoir si l'interception est possible il te faut calculer la valeur de y(x_J) et comparer le résultat obtenu à la valeur de H
Si  y(x_J) > H interception impossible car la balle passe trop haut
Si  y(x_J) <= H interception possible

Comment faire ?
a) Calculer   x_J ( Voir mon schéma)
b) Reporter la valeur de x_J dans l'équation de la trajectoire pour obtenir la valeur de y(x_J)
c) Comparer le résultat obtenu en b) avec H
d) Conclure

Question 3
y(XJ)=-g/2*x^2J+tan a*XJ+h
Est ce que y(XJ)=0 c est correcte où j ai tort

OK
J ai compris
S il vous plaît l abscisse du joueur
XJ=15 m
C est  ça ?

Oui

y(XJ)=-10/2*15^2+tan60*15+0,5
y(XJ)=-1125+16,7+0,5
y(XJ)=-1257,8

Non.
Il manque l'unité ( le mètre ) à ton résultat.
As tu remarqué que tu trouves que la balle se trouve à plus d'un kilomètre sous le sol du terrain de tennis ?
Il est impératif de vérifier la vraisemblance d'un résultat.
Une erreur de calcul est pardonnable.
Un résultat invraisemblable ne l'est pas !

-----------------------------------------------------------------------------------------------------

Puisque x_J = 15m on écrira y(x_J) sous la forme y(15) ce qui signifie " ordonnée de la balle ( en m )  quand son abscisse est égale à 15m "

A partir de l'équation de la trajectoire :


on aura



Je te laisse calculer y(15) et conclure.

y(15)=-9 ,8/2*14^2*cos^2(60)+225+25,98+0,5
y(15)=-9,8/392,5 +251,48
y(15)=251,45
Voici ma réponse

Ton résultat est faux, sans unité et invraisemblable.

y(15)=-9,8/98+225+25,98+0,5
y(15)=-0,1+251,48
y(15)=251,38 m

Je retombe sur la même réponse
y(15)=251,38 m

Bon ....
On va pas trainer deux heures là dessus .
y(15) = (-9,8/98)*225 + 25,98 +0,5 = - 22,5 + 25,98 + 0,5 = 3,98m
Il ne reste plus qu'à tirer la conclusion

Comme y(XJ)>H , l interception est impossible

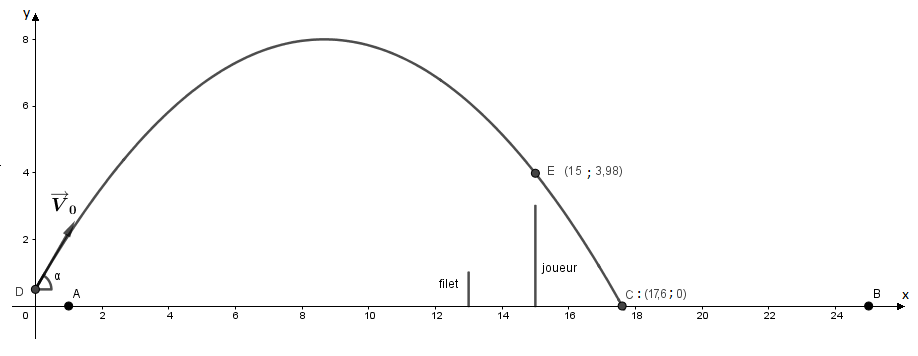
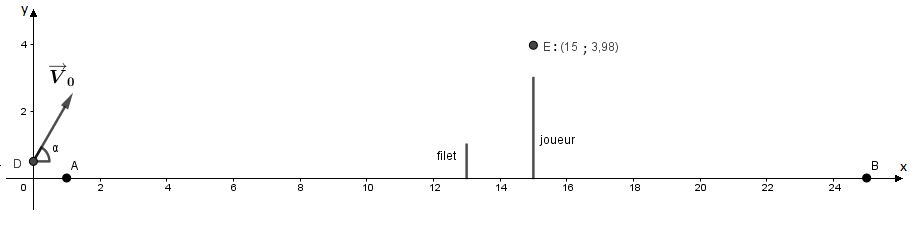
Oui, c'est bien ça, comme le montre le schéma ci-dessous.
La balle passe au point E près d'un mètre au dessus du sommet de la raquette du joueur.

Question 4
Oui la balle peut retomber dans l aire de jeu

Une chance sur deux pour que ce soit la bonne réponse.
Mais évidemment, sans justification, ton "pile ou face" n'a guère de valeur !

Je suggère d'appeler C le point de chute de la balle, de calculer la valeur de x(C), et de comparer le résultat avec x(B) (Voir schéma pour le point B)
Si tu trouves que x(C) < x(B) tu auras démontré qu'en effet la balle retombe bien dans l'aire de jeu.

Bonjour.
Avant de faire le calcul
X(C)=16 m.
C est ça

Non.

Comment faire ?

a) Remplacer dans l'équation y(x) de la trajectoire g, V₀, α et h par leurs valeurs numériques.
b) Le point C a une ordonnée nulle : Résoudre l'équation y(x) = 0 pour trouver l'abscisse x(C) du point C
c) Comparer x(C) et x(B) , Conclure

Bonjour
y(x)=-9,8/98*x^2+tan(60)*x+0 ,5
y(x)=-0,1x^2+1,73x+0,5
-0,1x^2+1,73x+0,5=0
∆=(1,73)^2-4*-0,1*0,5
∆=3,19
√∆=1,78
x1=-1,73+1,78/-0,2=-0,15 m
x2=-1,73-1,76/-0,2
x2=17,45
Comme x2>x(B)
Donc la balle ne retombe pas dans l aire de jeu

Le calcul est bien mené.
La précision du résultat est médiocre.
L'absence d'unité rend le résultat sans valeur.
La conclusion st fausse.

X2=17,45 m
Pourquoi la conclusion est fausse

J'ai trouvé x(C) = 17,6m
La balle retombe en C qui est situé  l'intérieur de la zone de jeu.
Ta conclusion est donc fausse.

Conseil pour ton topic Mouvement dans le champ g et E uniforme 6 :
Tu devrais joindre le schéma.

Merci infiniment

J aimerais savoir si je dois reprendre l exercice moi seul sans regarde la correction

C'est, me semble t'il, une excellente idée.