Inscription / Connexion Nouveau Sujet
mouvement dans le champ g et E uniforme 1
Bonjour a tous
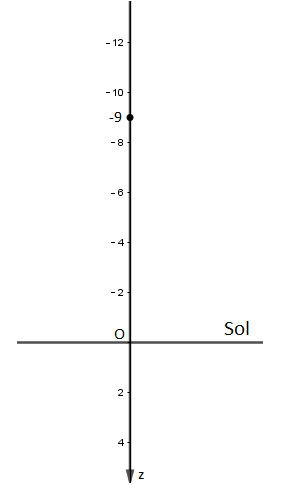
Une bille est lâche du deuxième étage d un immeuble a 9 mètre du sol , sans vitesse initiale .le sol est pris comme origine des espaces , l axe OZ étant orienté vers le bas.
1/ Établis l équation horaire du mouvement de la bille dans ce repéré .
2/ déterminer le temps que mettra la bille pour arriver.
Question1
Système : bille
Referentief: terrestre supposé galiléen dans le repéré orthonormé (OXy)
Appliquons le théorème du centre d inertie
P=ma
a=g est constant.donc le mouvement est uniformément variée
OM=1/2at^2+votre+VO
V=at+VO
Projections
a t=0, OMo[XO=0, y0=0]
a t différent de 0
Appliquons le théorème du centre d inertie
a=g=gZ[ax=0, ay=g]
OM[x(t)=0, y(t)=1/2*t^2+VO]
Question 2
y(t)=1/2 * t^2+VO
t=√(2y(t)/g)
t=√2*9/9,81
t=1,35 s
Voici ma proposition .
Je ne sais pas.
Je suis incapable de comprendre ce que tu écris.
L'équation horaire demandée à la question1 est :
z(t) = (1/2)*g*t² - h
Avec g = 9,8 m/s² et h = 9m
"Je voudrais savoir comment vous avez trouvé cette équation"
C'est la même que la votre, sauf que
- g ne passe pas à la trappe en passant d'une ligne à la suivante
- que la coordonnée selon l'axe Oz est appelé z et pas y
- que l'ordonnée à l'origine est notée h(comme hauteur) et non V0
- qu'il y a des exposants
...
a) Choix du système étudié, du référentiel et du repère :
On étudie la bille, référentiel terrestre, repère Oz vertical dirigé vers le bas (imposé par l'énoncé)
b) Recherche des forces extérieures qui s'exercent sur les système :
Une seule force : Le poids , vertical dirigé vers le bas et d'intensité P=mg
c) Application du théorème du centre d'inertie :
d) Projection sur le repère choisi :
a = g
e) 2 intégrations successives pour obtenir l'expression de la vitesse puis l'équation horaire en tenant compte qu'à la date t=0 l'énoncé impose v(0)=0 et z(0) = -h :
v(t) = gt
z(t) = gt²/2 - h
Question
J ai une question
Puis l équation horaire est
Z(t)=1/2*gt^2-h
Si je ne me trompe pas . comme le sol est pris comme origine des espaces
Donc
z(t)=0
Et bien si, tu te trompes.
z(t) = 0 voudrait dire que quelle que soit la valeur de " t " celle de " z " resterait nulle
En d'autres termes cela voudrait dire que la bille se trouverait au niveau du sol et y resterait.
A la date t=0 la bille se trouve 9 mètres au dessus du sol.
Puisque le sol est au niveau zéro et que l'axe Oz est orienté vers le bas cela signifie qu'à la date t=0 l'altitude de cette bille est de -9
En termes mathématiques cela se dit z(0) = -9