Bonjour, j'ai bloque sur un exercice.

On désire étudier le mouvement d'un projectile M, de masse m, lancé depuis le point O au sol.Pendant son “vol”, le projectile n'est supposé soumis qu'à son seul poids (on néglige toute forcede frottement). On se place dans le référentiel terrestre, supposé galiléen, que l'on munit d'un repère orthonormé(O,i,j,k), où k désigne le vecteur vertical ascendant (dirigé vers le haut).Les coordonnées du point M sont notées(x(t), y(t), z(t))

À t= 0, l'objet est lancé depuis le point Oavec une vitesse initial en →v0 de norme v0 et incliné d'un angle θ= (→i,→v0) par rapport à l'horizontale.

Pour les applications numériques, on prendra ces valeurs:

- norme de la vitesse initiale :v0= 15m/s
- inclinaison de la vitesse initiale par rapport à l'horizontale :θ= 20°
- accélération de la pesanteur :g= 9.81m.s-2(voir le paragraphe “aspects dynamiques”)
Tout le long du problème vous pourrez vérifier la cohérence des dimensions dans les expressions obtenues.

Etant donné la longueur du devoir, je mettrai chaque deux parties au fur et à mesure de mon avancée.

I/ aspects cinématiques :

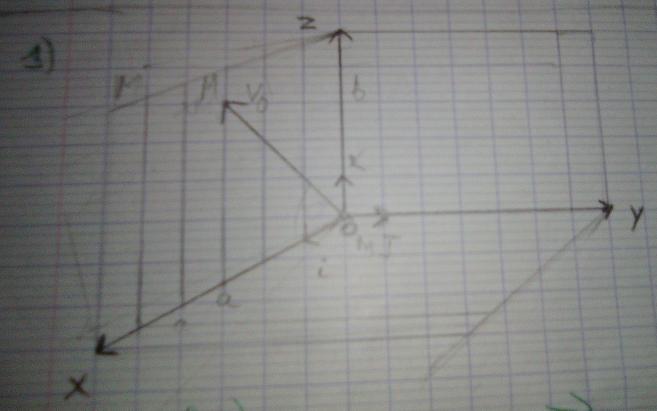
1)Faire un schéma. On désire exprimer la vitesse initiale sous la forme→v0=ai+bk.
Exprimer a et b en fonction de v 0 et de θ. Application numérique : Donner ensuite des valeurs numériques approchées de a et b.

2)Exprimer le vecteur →OM en fonction des coordonnées x, y, et z, et des vecteurs →i,→j, et →k.

3)En écrivant le vecteur position à l'instant t, et à l'instant t+dt(où d test une durée courte),et en écrivant la définition de la vitesse
v(t)= dOM/dt , montrer que: →v(t) =x′(t)i+y′(t)j+z′(t)k

On admet de même l'expression de l'accélération :

→a(t)=dv/dt= x′′(t)~i+y′′(t)~j+z′′(t)~k

II/ aspects dynamiques :

On admet que sous ces conditions, le mouvement est entièrement déterminé par la deuxième loi de Newton : ma=→P , où→P= −mgk est le poids de l'objet.

4)On faisant successivement le produit scalaire de la deuxième loi de Newton par les vecteur→i,→j, et→k, montrer que les coordonnées x(t), y(t), et z(t), vérifient
x′′(t) = 0, y′′(t) = 0, z′′(t) =−g

utiliser la linéarité du produit scalaire, ainsi que le caractère orthonormé de la base(~i,~j,~k)

5)Déduire une propriété de la fonction x′(t), ainsi que l'expression de x′(t) en fonction de la vitesse initiale

6)Déduire l'expression de x(t) en fonction de la position initiale.

7)Déterminer de même les expressions de y′(t), puis de y(t), et montrer que le mouvement s'effectue entièrement dans le plan y= 0.

8)Déterminer de même z′(t) puis z(t)

9)En étudiant les variations de z(t), montrer que l'altitude atteint un maximum zmax=  b2/2g  en un instant t1 que l'on déterminera.

remarque : Cette expression donnée de zmax doit être pour vous l'occasion de vérifier et éventuellement corriger vos calculs précédents.

10)Application numérique : calculer zmax et t1 pour les valeurs proposées dans l'énoncé.

11)Déterminer l'instant t2 où M touche le sol, ainsi que la portée p=x(t2) du jet (distance maximale parcourue au sol).

Application numérique : calculerp et t2 pour les valeurs proposées dans l'énoncé.

Nous verrons la suite plus tard...

Pour la 1, je fais mon schéma et je pars du principe que a=Cos (O).V0 et b= Sin (O).V0


2/ Dans notre situation t0, j'imagine que OM (0i, 0j, 0k)

3/ Je bloque sur la démonstration

4/ Pour la 4, je dois multiplier i, j, k avec P ou avec ma ?

Je vous remercie d'avance pour votre aide.