Inscription / Connexion Nouveau Sujet
Mouvement circulaire et force statique
Bonjour à tous,
Je me permets de poster ici, car je ne m'en sors pas avec un exercice dont voici l'énoncé (je traduis de l'anglais, en principe tout est correct) :
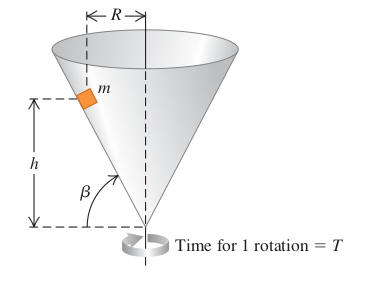
Un petit bloque de masse m est placé à l'intérieur d'un cône renversé en rotation autour d'un axe vertical de façon à ce que la durée d'une révolution du cône soit T. Les parois du cône forment un angle  avec l'horizontale. Le coefficient de friction statique entre le bloque et le cône est
avec l'horizontale. Le coefficient de friction statique entre le bloque et le cône est  s. Si le bloque reste à hauteur constante par rapport au sommet du cône, quelles sont a) la valeur maximum de T, et b) la valeur minimum de T ? (Autrement dit, trouvez les expression de Tmax et Tmin en fonction de
s. Si le bloque reste à hauteur constante par rapport au sommet du cône, quelles sont a) la valeur maximum de T, et b) la valeur minimum de T ? (Autrement dit, trouvez les expression de Tmax et Tmin en fonction de  et h). (J'ai joint un schéma illustrant le problème à la fin du message.)
et h). (J'ai joint un schéma illustrant le problème à la fin du message.)
J'obtiens facilement l'équation qui donne la forme générale du problème :
A partir de ac = (4 2R)/T2
2R)/T2
on obtient T = 2
 (R/ac)
(R/ac)
1) Pour obtenir R en fonction de  et h :
et h :
Soit un repère orthogonal (O, x, y)
soit un triangle rectangle dont l'hypoténuse est la génératrice c du cône, qui forme un angle  avec l'axe x. Le sommet du triangle correspondant au sommet du cône est le point O. La hauteur h est sur l'axe y.
avec l'axe x. Le sommet du triangle correspondant au sommet du cône est le point O. La hauteur h est sur l'axe y.
cos  = R/c donc R = cos
= R/c donc R = cos  . c
. c
sin  = h/c donc c = h / sin
= h/c donc c = h / sin 
Et donc R = cos  . h/sin
. h/sin  = cot
= cot  . h
. h
2) Les choses se corsent lorsqu'il s'agit d'obtenir ac.
Les forces qui agissent sur l'objet sont la force normale N, le poids w et la friction statique  s.
s.
La question est : comment ces forces s'additionnent pour donner une force centripète Fc qui soutienne ac ?
Je vois bien que les vecteurs N et w s'additionnent pour donner un vecteur qui pointe vers le sommet du cône (qui 'descend' le long de la pente) et qui participe à la force centripète (si je puis m'exprimer ainsi), par contre je ne sais vraiment pas quoi faire de la friction statique.
Je suppose que la friction statique joue un rôle double : 1) empêcher l'objet de glisser le long de la paroi du cône (vecteur parallèle à la génératrice dans un sens opposé au sommet), 2) empêcher l'objet de "sortir" du cône, donc en jouant le rôle de force centripète. (vecteur parallèle à la génératrice, orienté vers le sommet du cône, dont la composante x s'additionne à la force centripète).
Je comprends que plus la vitesse est élevée (donc plus T tend vers Tmin), plus la force centripète sera élevée, et plus la friction empêchant l'objet de sortir du cône sera élevée (la force normale étant quant à elle constante). Inversement, plus T tend vers Tmax, plus la friction empêchant l'objet de sortir du cône sera faible.
C'est à partir de là que se présente ma difficulté, je n'arrive pas à avoir une idée cohérente de la façon dont la (les ?) friction(s) interviennent pour s'additionner à la force centripète déjà donnée par la force normale et le poids.
J'ai tenté l'exercice, j'obtiens une partie de l'équation finale, mais il me manque des données. Mon message est déjà assez long, donc je ne vais pas vous embêter avec mes tentatives ratées, qui ne feront que rendre le message plus confus qu'il ne l'est déjà, d'autant qu'il me semble que ma difficulté centrale est exposée ci-dessus : que faire de la friction statique ?
Merci pour votre lecture, dans l'espoir de vous lire et de recevoir vos éclairages et vos idées,
Cordialement,
Bonjour,
Les forces qui agissent sur l'objet sont la force normale N, le poids w et la friction statique.
Oui, et on connait le mouvement, donc ici l'acceleration est centripète et connue en fct de v donc de T.
C'est toujours la même procédure:
- choix du référentiel, du repère
- bilan des forces
- 2e loi de Newton (donc ici 2 relations)
et ici en plus, aussi les lois du frottement (lois de Coulomb)
on devrait obtenir une condition sur l'acceleration.
Merci Krinn.
Voici ce que j'obtiens pour Tmin.
Tmin = 2
 (cot
(cot .h/ac)
.h/ac)
Pour les forces agissant sur l'objet (j'ai joint un schéma) :
 F =
F =  + vec(n) + vec (fs) = m . vec(ac)
+ vec(n) + vec (fs) = m . vec(ac)
Fc= m . ac = mg (sin +
+  s.cos2
s.cos2 )
)
donc ac = g (sin +
+  s.cos2
s.cos2 )
)
Donc
Tmin = 2
 [cot
[cot . h / g cos
. h / g cos (sin
(sin +
+  s.cos
s.cos )] = 2
)] = 2
 [ h / g sin
[ h / g sin (sin
(sin +
+  s.cos
s.cos )]
)]
Ce résultat ressemble (un peu) à la réponse correcte mais n'est donc pas la réponse correcte qui est
2
 [ h(cos
[ h(cos -
-  s sin
s sin ) / g tan
) / g tan (sin
(sin +
+  s cos
s cos )]
)]
Donc je suppose qu'il y a quelque chose qui ne va pas dans la manière dont je joins la friction statique à l'équation, mais je me creuse la tête depuis hier et je ne trouve pas.
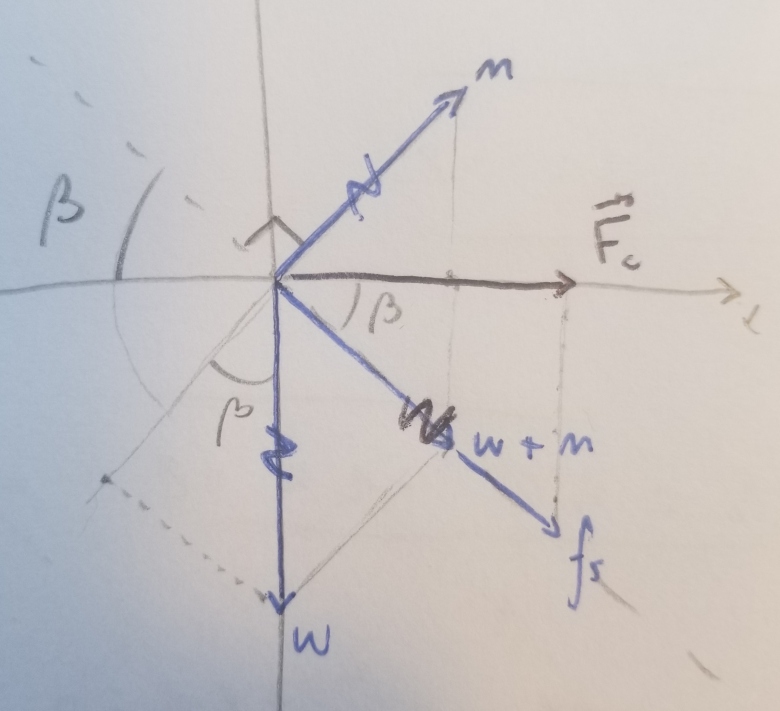
Pour les forces agissant sur l'objet (j'ai joint un schéma) :
 F =
F =  + vec(n) + vec (fs) = m . vec(ac)
+ vec(n) + vec (fs) = m . vec(ac)Oui, si tu choisis le ref. terrestre supposé galileen pour faire l'etude (il FAUT le preciser!)
Fc= m . ac = mg (sin
 +
+  s.cos2
s.cos2 )
)
Donc ac = g (sin
 +
+  s.cos2
s.cos2 )
)Non, je pressens une confusion: qu'appelles-tu Fc?
De plus ac depend de T.
Donc je suppose qu'il y a quelque chose qui ne va pas dans la manière dont je joins la friction statique à l'équation, .
Ce qui ne va pas, c'est que tu n'appliques pas la 2e loi de Newton mais tu essaies de deviner ce que donne la somme N+P par ex. (elle n'est pas colineaire à f)
Il faut projeter toutes les forces sur les axes et appliquer la loi.
Et ici il faut ensuite calculer |f/N| pour appliquer les lois de Coulomb et trouver des conditions sur a.
voici un schema possible: