Inscription / Connexion Nouveau Sujet
Moments
Bonjour à tous,
Je bloque sur un sujet de statique. Je cherche en vain depuis un bon moment.
Peut-être pourriez vous m'aider ?
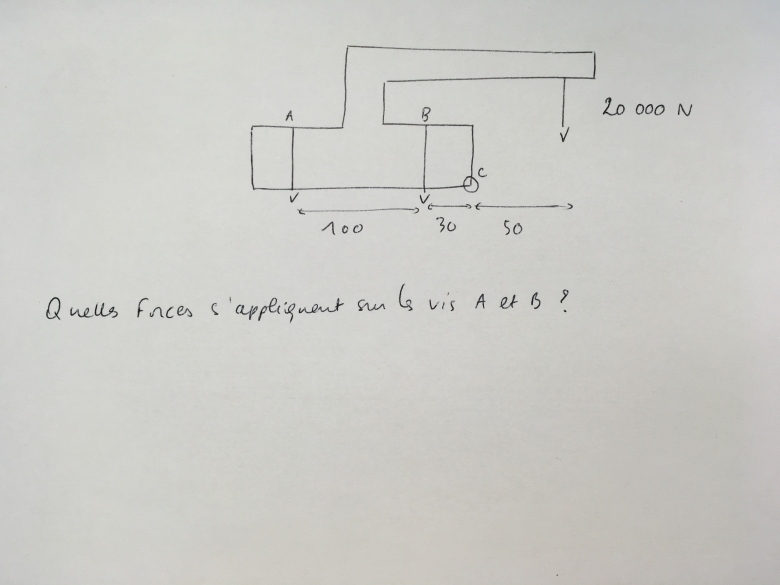
Voici l'énoncé : Cf. photo
Merci beacoup
Bonjour
Tu peux choisir comme système le solide en équilibre par rapport à la terre.
Quelles sont les forces exercées sur ce solide ?
Quelles sont les relations entre ces forces que tu peux déduire des conditions d'équilibre ?
Je n'ai aucune autre information sur le sujet.
Je sais que la poutre est en équilibre.
Mais je ne vois pas comment me dépatouiller de ça...
La demande est de déterminer les forces exercées sur les vis A et B.
Peut-être manque-t-il des informations dans l'énoncé ?
Suite à la remarque de Candide :
le fait que tu ais entouré d'un cercle le point C a-t-il une signification particulière ? Il ne s'agirait pas par hasard d'une charnière se comportant comme un axe de rotation ? Si les réponses à ces questions sont non, il n'y a pas de problème particulier. J'imagine que dans ce problème, l'influence du poids est négligé.
Je l'ai entouré car il s'agissait pour moi du point du moment.
Dans les deux cas de figure, quelles sont les pistes pour résoudre cet exercice ?
Merci
En d'autres termes, s'il n'y a pas de "charnière" ou axe de rotation, comment régler ce problème ?
Et dans le cas ou le point C serait l'axe de rotation du moment, comment aborder ce problème ?
Dans ces conditions, on peut, en négligeant le poids, considérer que le solide est soumis à trois forces :
Une force de vecteur exercée sur le solide par la vis en A ;
Une force de vecteur exercée sur le solide par la vis en B ;
Une force de vecteur exercée par la charge telle que F=2.104N
Commence par schématiser la situation en représentant les vecteurs forces ...
Que dire ensuite de la résultante des trois forces ?
Que dire ensuite de la somme algébrique des moments de ces trois forces par rapport à un axe fictif de rotation perpendiculaire au plan de figure et passant par C ?
Imaginons que cette pièce soit posée sur sa surface et que la partie droite en dehors du point C soit dans le vide.
Ce poids va créer un moment au point C.
La demande étant de déterminer les forces sur les vis A et B.
Tu n'est pas obligé de faire une figure à l'échelle. Seuls importent pour les calculs qui vont suivre, les directions et les sens des vecteurs force.
Mon moment au point C est de 10000Nm. En sachant ça, comment dois-je m'y prendre pour calculer les forces appliquées sur mes vecteurs A et B.
Nous n'en sommes pas encore à calculer les moments !
Essaie d'abord de répondre à mes question, en particulier à propos du schéma.
PS : cette modélisation est un simplification de la réalité car en pratique la table peut exercer des forces de contact et le poids du solide peut ne pas être négligeable mais cette modélisation simplifiée peut convenir à ce niveau...
Ta représentation n'est pas réaliste : tous les vecteurs ont la même direction et le même sens ; aucune chance d'obtenir une résultante de vecteur nul !
Pour trouver le sens de tu peux te demander se qui se passerait si les deux vis étaient enlevées et si la force
était appliqué...
On parle bien des forces que les vis exercent sur le solide. Pour empêcher le solide de pivoter autour d'un axe passant par C, la vis en A doit exercer sur le solide une force orientée vers le support. Pour le sens de l'action de la vis en B : toutes les forces ne doivent pas avoir le même sens comme déjà écrit. Voici une figure tenant compte de ces remarques. Cette figure n'est pas à l'échelle mais cela n'est pas gênant pour le raisonnement...
A toi maintenant d'appliquer les lois de la statique pour calculer FA et FB.
PS : les sens de vecteurs pourraient être obtenu de façon plus rigoureuse par un raisonnement algébrique mais bon : pour une première approche...
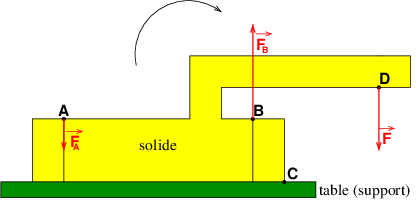
Merci vanoise pour cette illustration.
De manière spontanée, j'aurais dit que Fa et F ont des forces identiques.
Fb correspondrait à F+Fa.
Mais une fois cela énoncé ?
Je t'ai déjà fourni la méthode. Je me répète :
Que dire ensuite de la résultante des trois forces ?
Que dire ensuite de la somme algébrique des moments de ces trois forces par rapport à un axe fictif de rotation perpendiculaire au plan de figure et passant par C ?
La réponse aux deux questions posées va te fournir deux équations avec deux inconnues : FA et FB, les normes des vecteurs forces déjà définis.
Effectivement : la réponse à ma première question conduit à :
FB=FA + F .
Reste à écrire la seconde équation tenant compte des moments.
Bonjour,
Juste pour mon info ...
On étudie les systèmes hyperstatiques au lycée ?
Bonsoir,
En effet, deux vis devraient être assimilables à des liaisons encastrement, ce qui conduit de fait à un système hyperstatique => nilea71240 : cela signifie que tu ne pourrais pas avec ton niveau de connaissance résoudre cet exercice car tu as plus d'inconnues que d'équations. Mais c'est totalement hors programme dans le secondaire ...
J'imagine donc qu'ils assimilent chaque vis à un appui simple, ce qui revient à ce que suggère vanoise, à savoir :
1) Equation de la résultante statique selon l'axe vertical (Oy) ;
2) Equation du moment statique selon (Oz) en un point judicieusement choisi ...
Je vous laisse poursuivre ...
Bonne soirée !

Bonjour,
Juste pour mon info ...
On étudie les systèmes hyperstatiques au lycée ?
Bonsoir,
En effet, deux vis devraient être assimilables à des liaisons encastrement, ce qui conduit de fait à un système hyperstatique => nilea71240 : cela signifie que tu ne pourrais pas avec ton niveau de connaissance résoudre cet exercice car tu as plus d'inconnues que d'équations. Mais c'est totalement hors programme dans le secondaire ...
J'imagine donc qu'ils assimilent chaque vis à un appui simple, ce qui revient à ce que suggère vanoise, à savoir :
1) Equation de la résultante statique selon l'axe vertical (Oy) ;
2) Equation du moment statique selon (Oz) en un point judicieusement choisi ...
Je vous laisse poursuivre ...
Bonne soirée !

Merci pour ces précisions !
Pour le point 1) cela semble réglé
Vient ensuite le point 2)
Si j'ai bien compris :
(Fb * distance jusqu'à C) - (Fd * dis. C) - (Fa * dis. C) ?
Encore une question gbm, si ce sont effectivement des vis et qu'il faut les dimensionner, nous avons donc plus d'inconnus que d'équations, aurais-tu la gentillesse de me donner ta façon de faire ?
Merci beacuoup
La force de vecteur tend à faire tourner le solide d&ans le sens indiqué sur ma figure. Son moment est positif.
Remarque : il faut garder la même notation pour une même grandeur, sinon, on s'y perd très vite ! Avec les notations de la figure que j'ai fournie :
50.F-130.FA+30.FB=0
avec comme déjà écrit :
FB = F + FA
Puisque la valeur de F est connue, cela donne bien un système de deux équations à deux inconnues.
Si je souhaites calculer l'arrachement des deux vis A et B, par rapport au moment C, je dois m'y prendre autrement ?
D'ailleurs, j'en perds toute logique, l'arrachement sera plus fort sur la vis A ou B ?
La force de vecteur
Remarque : il faut garder la même notation pour une même grandeur, sinon, on s'y perd très vite ! Avec les notations de la figure que j'ai fournie :
50.F-130.FA+30.FB=0
avec comme déjà écrit :
FB = F + FA
Puisque la valeur de F est connue, cela donne bien un système de deux équations à deux inconnues.
Sens horaire, moment négatif ? ou je me trompe encore ?
Je pensais que le moment est positif lorsque la force produit une rotation dans le sens antihoraire.
Si je souhaites calculer l'arrachement des deux vis A et B, par rapport au moment C, je dois m'y prendre autrement ?
D'ailleurs, j'en perds toute logique, l'arrachement sera plus fort sur la vis A ou B ?
C'est une convention que l'on peut changer. On arrivera au final au même résultat. Fait comme tu as l'habitude de faire à condition de clairement indiquer la convention de signe choisie.
Pour être encore plus précis : avec le sens positif de rotation choisi sur mon schéma, j'ai obtenu :
50.F-130.FA+30.FB=0
Si tu inverses le sens positif de rotation, tu vas obtenir :
-50.F+130.FA-30.FB=0
Crois-tu que cela va changer quelque chose dans la détermination de FA et FB ?
Effectivement !
Merci pour ces précisions.
Suite à cela, pouvez-vous me donner des pistes sur ma demande ?
Si je souhaites calculer l'arrachement des deux vis A et B, par rapport au moment C, je dois m'y prendre autrement ?
D'ailleurs, j'en perds toute logique, l'arrachement sera plus fort sur la vis A ou B ?
Pour des compléments d'info concernant le message de gbm, je le laisse répondre lui-même.
En attendant, tu pourrais peut-être résoudre le système de deux équations à deux inconnues et obtenir les valeurs de FA et FB.
Bonjour,
Je ne sais pas non plus à quoi ça correspond la liaison en C, c'est le problème d'avoir un énoncé incomplet depuis le début : s'il s'agit d'un "axe de rotation" de type liaison pivot, cela introduirait deux efforts inconnus en plus et cela reviendrait à ce qu'à dit Candide dès le début.
Concernant le calcul d'arrachement de la vis, il existe plein de ressources en ligne mais cela fait appel à des notions que tu n'as jamais vues en résistance des matériaux.

Bonjour gbm
Comme tu le sais, je ne suis pas du tout spécialiste de RDM mais il me semble que, tout en restant dans le cadre du programme de première, et dans le cadre de la modélisation très simplifiée que j'ai proposée, on peut appliquer le principe des actions réciproques et ainsi s'intéresser aux forces :
et
Cela répond partiellement aux problèmes d'arrachement des vis.


