Inscription / Connexion Nouveau Sujet
Métronome
Bonjour, SVP veuillez m'assister ici.
Problème
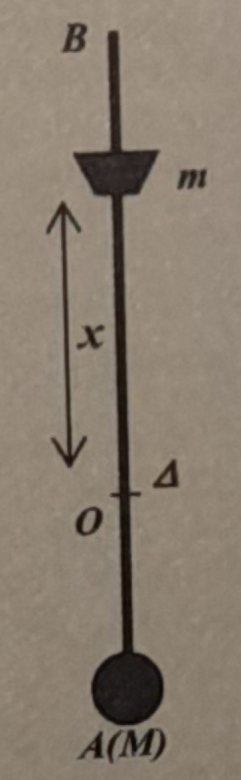
Un métronome, est constitué d'une tige AB, de longueur l, de masse négligeable mobile autour d'un axe horizontal (
). L'axe coupe la tige en O. En A est fixée une masse ponctuelle M = 60 g. Entre O et B peut se déplacer une masse ponctuelle m = 20 g. On donne :
AB = l = 30 cm ; OA = 10 cm ;
x = distance de l'axe de rotation à la masse m.
1) Si G est le centre d'inertie du pendule ainsi constitué, exprimer la distance a du centre de gravité G à l'axe de rotation.
2) Exprimer le moment d'inertie du pendule par rapport à ().
3) Donner l'expression de la période T des petites oscillations du pendule en fonction de x. Tracer la courbe T² = f(x)
Bonjour,
Je demande, puisque la masse m se déplace, le centre d'inertie G du pendule doit aussi se déplacer, c'est-à-dire G varie en fonction de x.
C'est ça ?
Bonjour,
Je demande, puisque la masse m se déplace, le centre d'inertie G du pendule doit aussi se déplacer, c'est-à-dire OG varie en fonction de x.
C'est ça ?
Un métronome est destiné à battre la mesure en musique. Sa période doit donc être réglable en fonction du rythme du morceau joué. Ce réglage s'obtient en modifiant la valeur de x. Cela modifie à la fois la valeur de a=OG et la valeur du moment d'inertie par rapport à l'axe, donc cela modifie la période.
D'accord.
J'utilise une relation barycentrique :
Soit G le barycentrique du système de A affecté de M et de B affecté de m. Alors :
En introduisant le point O, J'obtiens :
Les points O, G, A et B sont alignés. En module :
Or OG = a et OB = AB - OA = l - OA
Donc
AN : a = OG = 12,5 cm
C'est ça ?
Non : la masse "m" est à la distance "x" de O, pas à la distance OB. Relis bien mon message précédent : a=OG doit dépendre de x...
Attention : le point G doit nécessairement être situé entre O et A.
OK.
Soit C un point situé entre O et B tel que OC = x. La masse m est en C.
J'utilise une relation barycentrique :
Soit G le barycentrique du système de A affecté de M et de C affecté de m. Alors :
En introduisant le point O, J'obtiens :
Les points O, G, A et C sont alignés. En module :
Or OG = a et OC = x
Donc
C'est ça ?
Non : et
sont des vecteurs de même sens mais
et
sont des vecteurs de sens opposés. Il faut en tenir compte dans les projections.
D'accord.
2) Expression du moment d'inertie du pendule par rapport à l'axe Delta :
La masse de la tige étant négligeable, le moment d'inertie du pendule est :
J = Jm + JM
Avec Jm = m.x² et JM = M.OA²
Donc
L'énergie mécanique du pendule est :
Em = Ec + Epp
• L'énergie cinétique du pendule est Ec = ½J.
²
Or = d
/dt = 
'
Donc Ec = ½J.'
• Pour l'Epp, choisissons un axe vertical orienté vers le bas dont l'origine coïncide avec le point O
Epp = - (M+m)gh ( avec h = a.cos)
Donc Epp = - (M+m)ga = - (M+m)g.a.cos
Ainsi Em = ½J.' - (M+m)g.a.cos
Or l'Em = constante, sa dérivée par rapport au temps est nulle.
Est-ce que je suis sur la bonne voie ?
L'énergie mécanique du pendule est :
Em = Ec + Epp
• L'énergie cinétique du pendule est Ec = ½J
.²
Or
= d/dt = '
Donc Ec = ½J
.'
• Pour l'Epp, choisissons un axe vertical orienté vers le bas dont l'origine coïncide avec le point O
Epp = - (M+m)gh ( avec h = a.cos
)
Donc Epp = - (M+m)gh = - (M+m)g.a.cos
Ainsi Em = ½J
.' - (M+m)g.a.cos
Or l'Em = constante, sa dérivée par rapport au temps est nulle.
Est-ce que je suis sur la bonne voie ?
Oui ; tu as déjà fait ce raisonnement dans d'autres problèmes postés récemment. Étourderie sans doute : tu oublies parfois le carré pour la vitesse angulaire dans l'expression de Ec.
Je me trompe très souvent en oubliant le carré de la vitesse. Mais, désormais je vais y veiller. Merci.
Em = ½J'² - (M+m)g.a.cos
dEm/dt = 0 
J.''' + (M+m)g.a.'sin = 0
Or est faible, donc sin 
Donc
Alors est la pulsation propre du pendule.
La période propre est
C'est cela ; il te reste à remplacer "a" et J par leurs expressions en fonction de x puis à tracer la courbe demandée.
D'accord.
Alors
Après simplification, J'obtiens :
. En faisant l'application numériques, je trouve :
Je pense que tu as oublié d'élever (OA) au carré au numérateur de ton expression.
Pour le tracé, il faut remarquer :
0
x 0,20 (x en mètre).
D'accord, mais je suis un peu retissant, mon expression de T² n'est pas homogène en terme d'unité
C'est bon. Je m'étais trompé en vérifiant l'homogénéité de l'expression de T². Elle bien homogène !
Maintenant, quand je fais l'application numérique, je trouve T² en fonction de x (en mètre). Un mélange d'application numérique et d'expression littérale, finalement je me retrouve avec T² non homogène.
Tes formules littérales sont homogènes. Impossible de contrôler l'homogénéité à la dernière formule car mélange de valeurs littérales et numérique mais il faut procéder ainsi selon l'énoncé.
A mon avis : revoir le 0,3 du numérateur.
Pour le tracé de la courbe T² = f(x), je fais un tableau de valeurs, sachant que 0 x 20
| x (en mètre) | 0 | 0,10 | 0,20 |
| T² (en s²) | 0,395 | 0,789 | 2,763 |
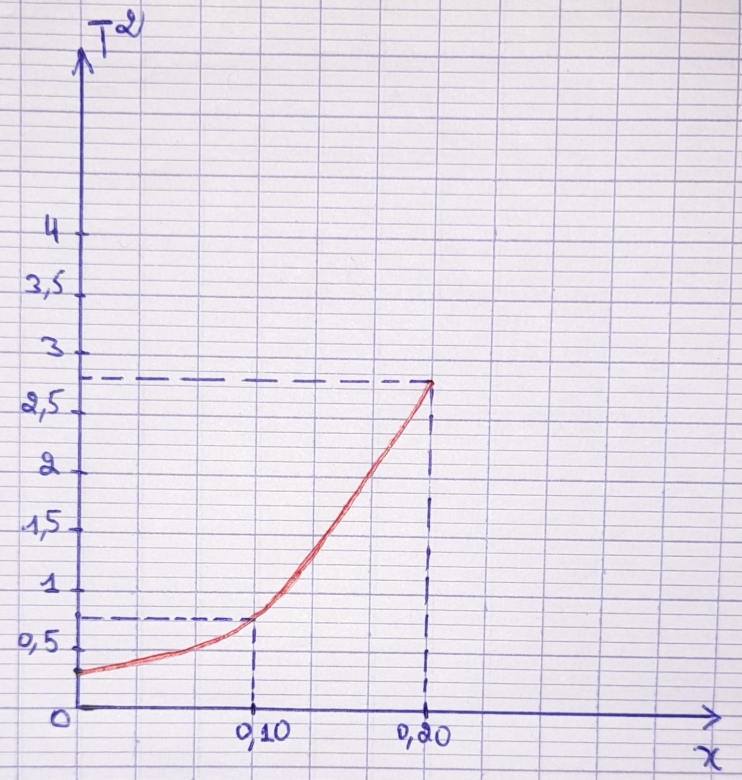
L'allure générale est bonne. Tu aurais pu sans doute ajouter quelques points pour une meilleure précision.
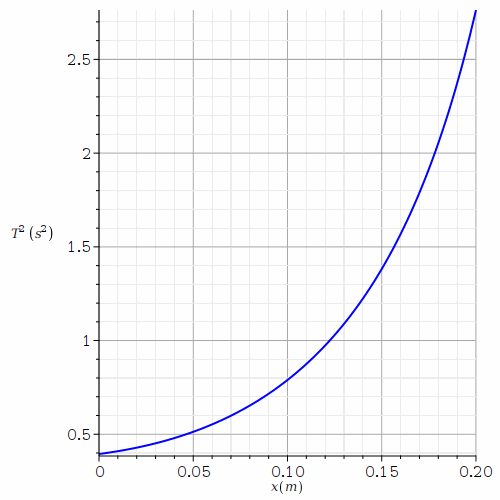
Non bien sûr. Le zéro que tu vois concerne seulement les abscisses. Regarde bien . L'ordonnée en x=0 est un peu inférieure à 0,40s2 ; on retrouve le 0,395s2 de ton tableau.
Annuler
connectez vous