Inscription / Connexion Nouveau Sujet
Mécanique : forces dans un plan incliné
Bonjour,
Je bloqué sur l'expression des coordonnées de forces dans un plan incliné :
Une skieuse de masse m = 60 kg est accrochée à la perche d'un téléski et se déplace avec une vitesse de valeur constante. Le téléski exerce sur la skieuse une force constante F dans l'axe de la perche. Les forces de frot tement exercées par l'air et par la neige sont négligées.
1. Établir l'inventaire des forces exercées sur la skieuse et représenter l'ensemble de ces forces sans souci d'échelle au centre de masse G de la skieuse.
a. Faire le bilan des forces s'exerçar Les représenter sur un schéma sans soucis d'échelle
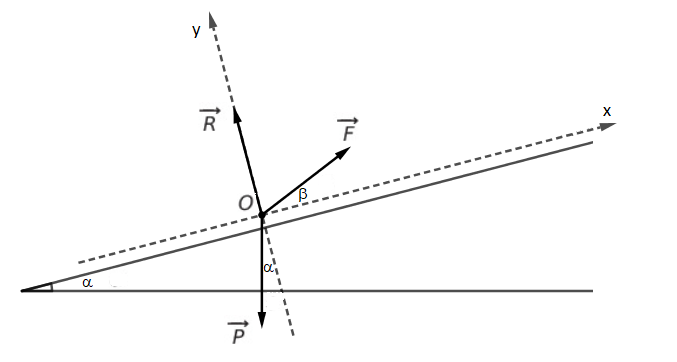
Il y a le poids P ( direction : perpendiculaire à l'horizontale, sens : vers le bas), la réaction normale du support (perpendiculaire à la piste dirigée vers le haut selon l'axe Oy) et la force constante exercée par la perche sur le skieur (direction axe de la perche)
2. Exprimer les coordonnées de chacune des forces dans un repère cartésien (O;i, j) dont l'axe Ox est parallèle à la pente.
Alors R (0;R)
Je pense que P (-Pcos (alpha) ; - Psin (alpha) et que F (Fcos (Beta-Alpha) ; F sin (Beta-Alpha)
3. Calculer la valeur F de la force exercée par la perche sur la skieuse.
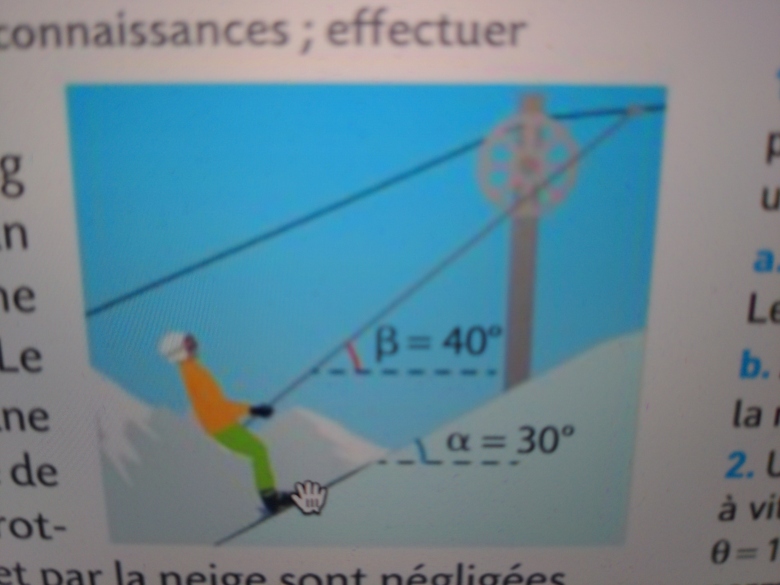
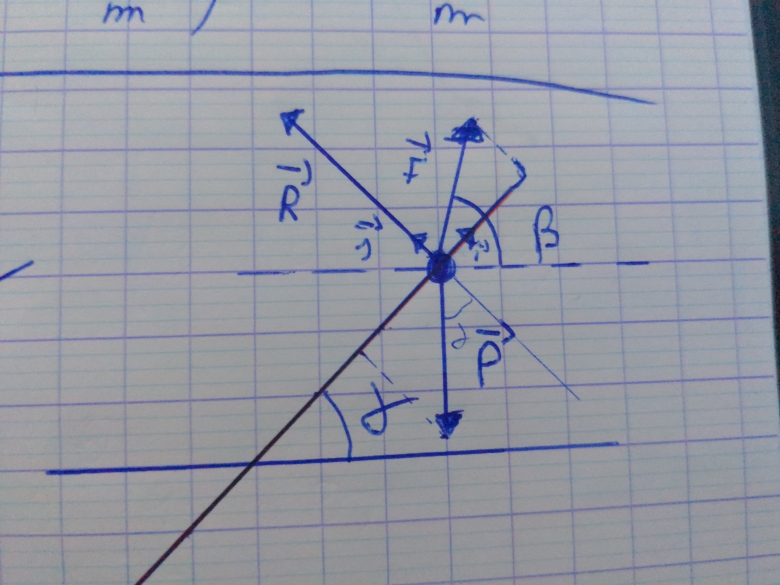
Mais l'angle Beta est par rapport à l'horizontale, pas par rapport à la piste, non ? selon le schéma de l'énoncé
Pour le poids :
cos (A) = Px / P donc Px = -Pcos (A)
sin (A) = Py/ P donc Py = -Psin(A)
Tu as raison en ce qui concerne l'angle β : Je n'avais pas regardé avec suffisamment d'attention la figure fournie par l'énoncé.
J'ai corrigé mon schéma en conséquence.
En revanche je ne suis pas d'accord avec toi pour le vecteur poids.
Pour moi :
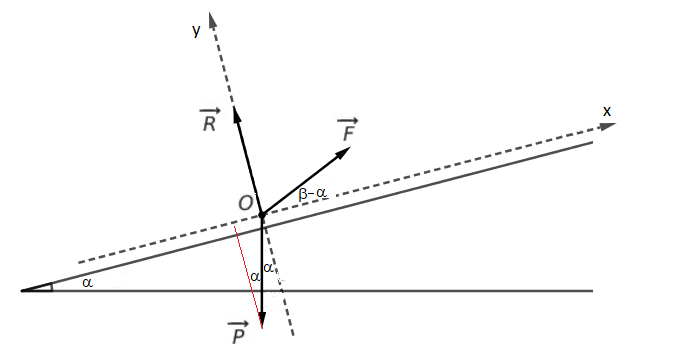
et donc :
- P cos (alpha) + Fsin (beta-alpha) =0
F sin (beta -alpha) = P cos (alpha)
F = Pcos (alpha) / sin (beta-alpha)
F= 298, 8 N
Je n'obtiens pas la même relation ( entre F, P, α et β ) que toi, mais j'obtiens le même résultat numérique ce qui est évidemment anormal.
j'ai trouvé :
Sur Ox :
-P*sin(α ) + F*cos( β - α ) = 0
F = P * sin(α ) / cos ( β - α ) = m * g * sin(α ) / cos ( β - α )
AN:
F = 60 * 9,8 * sin (30) / cos ( 40 - 30 )
F = 298,5N qu'on arrondit à 3,0.102 N ( 2 chiffres significatifs )