Inscription / Connexion Nouveau Sujet
Mécanique (exercice skieur)
Bonjour j'ai quelques questions sur un exercice:
Un skieur de 80 kg descend une piste de 150 m inclinés de 20° par rapport à l'horizontale.
Déterminer sa vitesse en considérant deux cas de figure:
1) On néglige les frottements sur les skis
2) On prends en compte la force de frottement des skis qui vaut 150 N.
On néglige la résistance de l'air.
J'ai commencé la question 1
Pour cela j'ai marqué que les forces qui s'appliquent sur le skieur sont le poids P et la réaction de support de la piste R, j'ai fait un schéma avec un système d'axe en mettant Ox=longueur de la piste et Oy=dans le même sens que R
La suite j'était perdu alors j'ai regardé la correction qu'avait donné la prof
Elle a mis Ox= P sin  OK
OK
Oy= R+P cos  OK
OK
Et ensuite Ay=0. Pourquoi??
Merci d'avance pour vos réponses (je tient à préciser que je commence à peine la méca ,comprenez que je suis un peu perdu...)
Bonjour,
Question 1
Je ne comprends pas grand chose à la correction de ton professeur.
Le skieur est soumis à deux forces :
Son poids
La réaction de la piste :
Le mouvement est étudié dans un référentiel terrestre, donc supposé galiléen.
La deuxième loi de Newton stipule que :
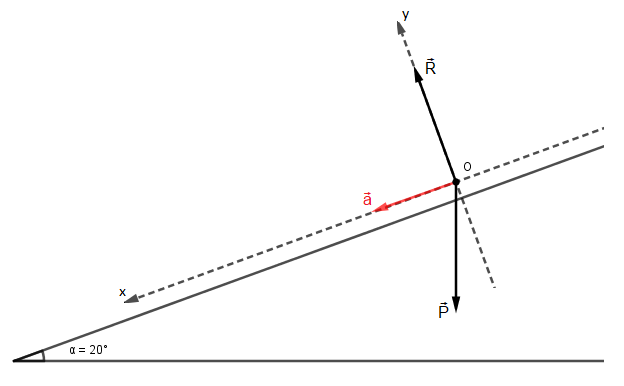
En projetant cette relation vectorielle sur un repère Ox, Oy (Voir figure ) on obtient deux relations algébriques.
Une des deux relations permet de calculer la valeur de l'accélération " a "
A partir de la valeur de " a " on pourra répondre à la question posée.
Remarque :
Puisque les frottements sont négligés on peut aussi appliquer la conservation de l'énergie mécanique.
Malheureusement l'énoncé ne dit rien de la vitesse initiale du skieur.
Et la question posée ne précise même pas à quel instant ( ou a quel endroit) il faut calculer la vitesse du skieur
j'ai mal copié déja Oy= R-P cos 
Ce qui est bizarre c'est que j'ai résolu la question 1 en utilisant juste l'axe Ox et la relation P* sin  en l'intégrant...
en l'intégrant...
Pourquoi l'axe Ay est nul etla réaction de support n'intervient pas? 
Du coup j'ai obtenu 1/2*g*t²*sin =x(t) en intégrant et après avoir trouvé le temps qui'il met pour arriver au bout j'ai j'ai injecté T=9,46s dans v(t)=g*t sin
=x(t) en intégrant et après avoir trouvé le temps qui'il met pour arriver au bout j'ai j'ai injecté T=9,46s dans v(t)=g*t sin .
.
Pourquoi l'axe Ay est nul etla réaction de support n'intervient pas?
Désolé, mais je ne sais pas ce que peut être un "axe nul"
2e loi de Newton :
Projections
Sur Ox : m g sin(α) + 0 = m a donc a = g sin (α) ce qui permet de calculer la valeur de " a "
Sur Oy : - m g cos (α) + R = 0 ce qui permet de calculer la valeur de R (qui n'est pas demandée)
Le vecteur accélération
Sur Ox : ax = a
Sur Oy : ay = 0
Il n'y a aucun mouvement selon l'axe Oy et c'est pourquoi la projection sur cet axe n'est pas utile pour l'étude du mouvement du skieur.
Le mouvement du skieur est uniformément accéléré. Son accélération est a = g sin(α)
On simplifie la fin du calcul en appliquant la relation V² - (V0)²= 2 a L ce qui évite d'avoir à calculer la valeur de la durée de la descente qui n'est pas demandée.
Bien que l'énoncé ne le précise pas je suppose que V0 = 0
V²= 2 g sin(α) L


