Inscription / Connexion Nouveau Sujet
mecanique du point
Bonjour à tous,
j'espère que vous pourrais m'aider avec cet exo:
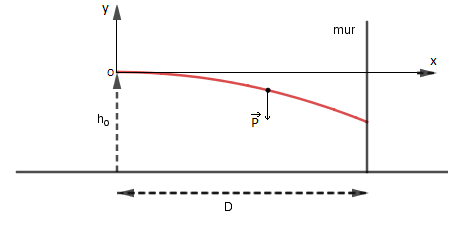
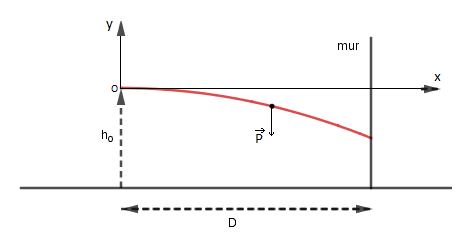
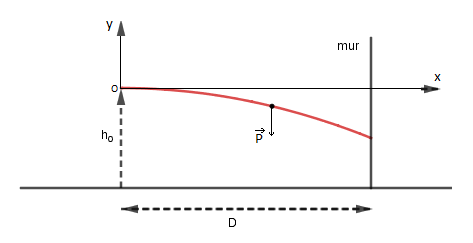
Un joueur de pelote lance une balle de masse m avec une vitesse initiale horizontale de norme V0, la balle est initialement à une distance horizontale D du mur et à une hauteur h0 du sol. Le référentiel terrestre est considéré galiléen. (𝑥 ⃗,𝑦 ⃗) est un repère orthonormé lié au référentiel terrestre, 𝑦 ⃗ est vertical ascendant.
1) Après avoir effectué un bilan d'effort(s) de la balle (considérée comme une masse ponctuelle non soumise au frottement de l'air), écrire le principe fondamental de la dynamique (PFD) appliqué à la balle.
2) En déduire l'expression du vecteur vitesse de la balle (composantes suivant 𝑥 ⃗ et 𝑦 ⃗)
3) En déduire l'expression du temps que mettra la balle à atteindre le mur.
4) Déterminer la hauteur de l'impact de la balle avec le mur.
5) Déterminer l'expression de la trajectoire de la balle y(x), on prendra l'origine de l'axe x à la position initiale de la balle.
voici mes réponses :
1/ seul le poids agit sur la balle donc pour résumé g=a
2/ ici on nous dit que la vitesse initiale est horizontal donc Vi aura une composante seulement sur x. du coup j'ai mis Vx=- 1/2gt carré
3/ le temps sera racine carré de Vx2/g
et pour la 4 et la 5 je n'y arrive pas.
je vous remercie d'avance pour votre aide
Bonjour,
Il s'agit d'un exercice très classique et tu trouveras facilement sur internet ( et même sur ce forum ) une multitude d'exercices équivalents.
Un conseil tout de même:
L'énoncé indique que le mouvement de la balle sera étudié dans un repère orthonormé dont l'axe vertical est ascendant, mais il ne précise pas la position de l'origine O de ce repère.
Deux possibilités intéressantes :
a) Soit tu situes ce point O au point de départ de la balle.
b) Soit tu choisis ce point O au niveau du sol à la verticale du point de départ de la balle.
Les deux choix sont possibles, mais il faut en faire un, car certaines équations vont dépendre de ce choix.
Ensuite pour répondre à la question 2 (Ce que tu as fait est faux) il te faut établir les équations donnant les composantes vx et vy du vecteur vitesse en fonction du temps.
vx = .................
vy = .................
ok merci.
est ce que je peux essayer de le refaire correctement et posté mes réponses pour que tu me corrige?
Bonjour,
est ce que je peux essayer de le refaire correctement et posté mes réponses pour que tu me corrige?
Oui, bien entendu ! C'est le but de ce forum.
Une remarque :
Le choix de la position du point O est libre et tu peux donc utiliser une des deux possibilités que j'évoquais dans mon précédent message.
Toutefois, à la question 5 ce choix est imposé :
"5) Déterminer l'expression de la trajectoire de la balle y(x), on prendra l'origine de l'axe x à la position initiale de la balle.
Il est alors peut être plus simple de l'adopter dès le début du problème.
Voir schéma ci-dessous.
Bonjour,
j'espère que tu vas bien je te montre un peux ce que j'ai fait:
1) g=a
2) ax=g ay=0
par intégration on en déduit:
vx(t)= gt+cste1 et vy(t)=cste2
or a t=0 on a:
vx= Vo et vy= 0
on en deduit les constante:
cste1=V0 et cste2=0
les équations horaire de la vitesse sont donc:
vx(t)=-gt+v0
vy(t)=0
3) on pose (vx(t)-v0)= t
t V/g
V/g
4) je n'ai aucune piste pour cette question
5)d'après les conditions initiales on a:
x0=0 et y0=h0
et donc x(t)=0 y(t)=-1/2gt[sup][/sup]+v0t+h0
voila j'espère vraiment qu'il y'a de bonnes réponses je suis autodidacte donc c'est pas évident de tous comprendre par soi même .
merci pour le temps que tu m'accorde
Bonjour,
Question 1 : Exact
Question 2 : C'est très bien, sauf tout à la fin ou tu as interverti vx et vy
Question 3 : En intégrant les équations de la vitesse, tu vas obtenir les équations x(t) et y(t) de la balle. Conformément à mon schéma j'ai pris l'origine des axes coïncidant avec la position initiale de la balle.
L'équation de x(t) permet de répondre à la question 3
L'équation de y(t) associée au résultat de la question 3 permet de répondre à la question 4
Question 5 : Il suffit d'éliminer la variable " t " entre x(t) et y(t) pour obtenir y(x)
Aie aie aie.
1)
Les forces agissant sur la balle sont son poids (vertical vers le bas et d'amplitude |mg|, les frottements de l'air sur la balle et la poussée d'Archimède de l'air sur la balle.
Comme la balle es considérée comme ponctuelle, les frottements de l'air sur la balle et la poussée d'Archimède de l'air sur la balle sont nuls et donc :
La seule force agissant sur la balle est son poids.
2)
La composante horizontale des forces agissant sur la balle est nulle et donc la composante horizontale de la vitesse est constante :
vx(t) = Vo
La composante verticale des forces agissant sur la balle est mg, dirigé vers le bas et la composante verticale de la vitesse en t = 0 étant nulle, on a :
ay(t) = -g
vy(t) = -g.t
Ce n'est pas du tout ce que tu as écrit ...
A toi de comprendre ce que j'ai écrit ci-dessus ... avant de continuer.
Sauf distraction. 
dsl j'ai mal lu ta réponse du coup j'ai refait au propre
1) la balle est considérée comme une masse ponctuelle non soumise au frottement de l'air. seul le poids de la balle agit sur la balle
d'après le PFD on  Fexterieur=m.a et donc mg=ma après simplification on obtient g=a
Fexterieur=m.a et donc mg=ma après simplification on obtient g=a
2)Le vecteur ~g est orienté vers le bas, dans le sens inverse à l'orientation de l'axe (O;y), un signe − apparaît:
ax =0 ay =−g Par intégration , on cherche désormais la vitesse. dv/dt = a
vx = C1
vy =−g·t+C2 avec C1 et C2 des constantes
Pour déterminer les constantes, on se situe aux conditions initiales. Ici, on sait qu'à l'instant (t =0), v(t=0)( vx (t=0) = v0 vy (t=0) = -gt
3) Cherchons maintenant l'équation horaire de la trajectoire de la balle. On sait que : dx/dt = vx et dy/dt = vy
En appliquant l'inverse de la dérivée, on trouve :
x = v0·t+ cste3
y =−1/2g·t[/sup] +cste 4 avec C3 et C4 des constantes à déterminer à partir des conditions initiales connues.
À t =0, x(0)=0 et y(0)= h0, donc C3 =0 et C4 = h0. Finalement :
x = v0·t y =−1/2g t[sup] +h0
en prenant l'expression de x on obtient t=x/v0
4)en prenant l'expression de y dans le résultat précèdent on obtient
h0=2y/gt[/sup]
5)Dans les expressions trouvées précédemment, la variable commune à x et y est t. On commence donc par exprimer t en fonction de x :
x = v0·t ⇔ t = x/v0 On injecte t dans y : y =−1 /2g·( x/v0)[sup] +h0
voila j'espère vraiment que cette fois ci c'est la bonne
Question 3 :
donc C3 =0 et C4 = h0.
Prendre C4=h0 revient à prendre l'origine du repère utilisé au niveau du sol, à la verticale du point de départ de la balle.
Ce choix est pertinent, mais il faut l'expliciter clairement.
en prenant l'expression de x on obtient t=x/v0
Les notations sont incorrectes.
 =D/v0
=D/v0 Question 4 :
Reprendre y = -(1/2)gt² + h0 à la date t =
 =D/v0
=D/v0
Question 5 : Attention l'énoncé impose de prendre l'origine des axes au point de départ de la balle.
t et x sont des variables qui peuvent au cours de l'exercice prendre différentes valeurs.
Mais cette question porte sur une valeur précise prise par t quand la balle arrive à une abscisse précise qui est celle du mur
Donc, ici, la variable x prend la valeur D au moment où la variable t prend la valeur 
 = D/v0
= D/v0


