Inscription / Connexion Nouveau Sujet
mecanique
Bonsoir de l'aide svp
On accroche une bille de masse m=200g au bout d'un fil de masse negligeable et de longueur l=1m.On lache la bille avec une vitesse nulle dans une position initiale faisant un angle θ=15◦ avec la verticale.
1)Quelle est la vitesse Vm lors de son passage par la position verticale?2)Etablir par deux methodes puis calculer la periode de ce pendule en supposant que le mouvement verifie l'hypothese des petites oscillations
La dernière question seulement
Merci d'avance
En 1ere ???
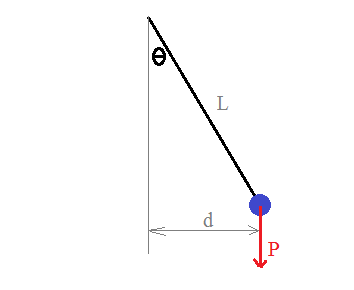
En considérant la masse comme ponctuelle :
Soit theta l'angle entre la verticale et la corde.
d = L.sin(theta)
C = P * d = m.g.L.sin(theta)
J = m.L²
C = -J.d²theta/dt²
m.g.L.sin(theta) = -m.L².d²theta/dt²
d²theta/dt² + g/L.sin(theta) = 0
Si theta est petit, on a sin(theta) theta
Et on a donc d²theta/dt² + g/L.theta 0
Equation différentielle donnant une réponse oscillatoire de pulsation
Or et donc :
Sauf distraction. 
Autrement :
En prenant la référence pour les Epp nulles à la position de repos de la masse.
E mécanique du système :
et pour theta différent de thetao, soit dtheta/dt la vitesse angulaire de la masse.
Em = mg.L*(1-cos(theta)) + 1/2.mL².(dtheta/dt)²
Conservation de l'énergie mécanique -->
mg.L*(1-cos(theta)) + 1/2.mL².(dtheta/dt)² = mg.L*(1-cos(theta_o)
g.L*(1-cos(theta) )+ 1/2.L².(dtheta/dt)² = g.L*(1-cos(theta_o)
On dérive par rapport au temps -->
gL.sin(theta).(dtheta/dt) + L².(dtheta/dt) * (d²theta/dt²) = 0
dtheta/dt n'est pas identiquement nul (comme le pendule oscille) -->
gL.sin(theta) + L².d²theta/dt² = 0
d²theta/dt² + g/L.sin(theta) = 0
... et on est revenu à une équation identique à la méthode précédente
Sauf distraction. 


