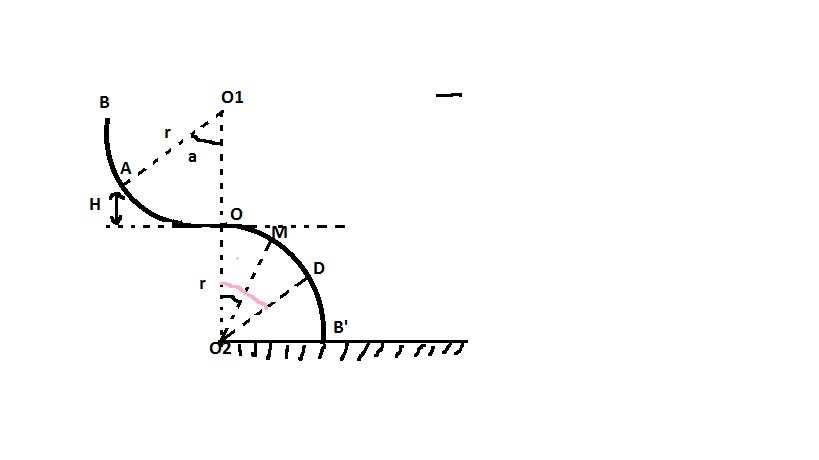Inscription / Connexion Nouveau Sujet
mecanique
Bonjour de l'aide svp. J
Une portion de gouttière BO de forme circulaire de rayon r=1m se situe dans un plan vertical. Elle se raccorde en O à une autre gouttière identique OB' située dans le meme plan(voir figure). Les centres O1 et O2 des deux gouttières se trouvce sur le meme plan horizontale passant par O . les frottement sont négligeables et g=10N/Kg
1) En choisissant le point O milieu de O1O2 comme origne ds altitudes et comme position de reference. Calculer l'energie mecanique du solide ;
2) Exprimer puis calculer la vitesse VO du solide au passage en O
3) Sur le parcours OD le solide reste en contact avec la surface de la gouttière et sa posistion est reperée par l'angle  =(O2O, O2M).
=(O2O, O2M).
Etablir l'expression de la vitesse V du solide en un point M quelconque du trajet OD en fonction de h, r ,g et 
4) Sur le trajet OD on montre que l'intensité R de la reaction de la gouttière sur S a pour expression R=mg.(cos -v2/rg). Au point D le solide perd le contact avec la gouttière et suit le trajet DC. Determiner la valeur numerique
-v2/rg). Au point D le solide perd le contact avec la gouttière et suit le trajet DC. Determiner la valeur numerique  D de
D de  et celle de Vc au point D.
et celle de Vc au point D.
5) A quelle vitesse le solide touche til le sol en C
J'ai pu faire le 1, 2,3
merci d'avance
Bonjour.
Sur le trajet OD on montre que l'intensité R de la reaction de la gouttière sur S a pour expression R=mg.(cos
 -v2/rg). Au point D le solide perd le contact avec la gouttière
-v2/rg). Au point D le solide perd le contact avec la gouttière À vous.
Je présume que l'objet est laché à vitesse nulle du point B ... et que l'oblet glisse sans rouler tout sur l'entiéreté du trajet BD ...
Mais ces 2 précisions devraient IMPERATIVEMENT être fournies par l'énoncé.

Il manque une donnée.
D'où est laché l'objet ?
Je présume que c'est en A et pas en B.
Si oui, alors :
1)
Em = mgH
-----
2)
Conservation de l'émegie macanique :
mgH = 1/2.m.Vo² (avec Vo la vitesse en O)
Vo² = 2gH
Vo = RacineCarrée(2gH)
-----
3)
En M :
Epp = -mg.r(1-cos(theta))
Ec = 1/2.m.VM²
Em = 1/2.m.VM² - mg.r(1-cos(theta))
Conservation de l'énergie mécanique :
1/2.m.VM² - mg.r(1-cos(theta)) = mg.H
1/2.m.VM² = mg.r(1-cos(theta)) + mg.H
VM² = 2g.r(1-cos(theta)) + 2g.H
VM = Racinecarrée[2gr(1-cos(theta)) + 2g.H]
-----
4)
Au point D, R = 0 --> cos(theta) = VD²/(g.r)
VD = RacineCarrée[2gr(1-VD²/(g.r)) + 2g.H]
VD² = 2gr(1-VD²/(g.r)) + 2g.H
VD² = 2gr - 2VD² + 2g.H
3VD² = 2g.(r+H)
VD = RacineCarrée[(2/3).g.(r+H)]
cos(theta) = VD²/(g.r)
cos(theta) = (2/3).g.(r+H))/(g.r)
cos(theta) = (2/3).(r+H))/r
(Pour autant que (2/3).(r+H))/r <= 1)
Donc pour 2r + 2H <= 3r
H <= r/2
Si ce n'est pas le cas, alors l'objet décollera au point O
-----
5)
Conservation de l'énergie mécanique.
mg(H+r) = 1/2.m.VC²
VC² = 2g.(H+r)
VC = RacineCarrée[2g.(H+r)]
-----
Sauf distraction.