Bonsoir;
J'ai trouvé une définition :Expression de la loi de Wien

La loi de Wien s'applique aux sources chaudes ( aussi appelées corps noirs ) et permet de relier la température T d'une source chaude à la longueur d'onde de l'intensité lumineuse maximale λmax.
La loi de Wien peut s'écrire sous forme de la formule suivante:

λmax x T = 2,898 x 10-3    Dans cette formule λmax est en mètre T est en degré Kevin ( K ) La constante ( 2,898 x 10-3 )est en Kevin mètre ( K.m)

Le degré Kevin

Dans la loi de Wien la température s'exprime en degré kévin qui correspond à l'unité du système internationale. Cette température est aussi appelé température absolue et a comme origine la plus petite température qui puisse être atteinte: - 273 °C.
Si θ est la température exprimée en degré celcius et T la température exprimée en dégré Kevin alors la relation entre les deux est: T = θ + 273

En fait ce que j'ai pas compris c'est à quoi servent les corps noirs

Et voici une image je ne comprends pas bien comment interviennent les rayonnements,que montrent-ils?

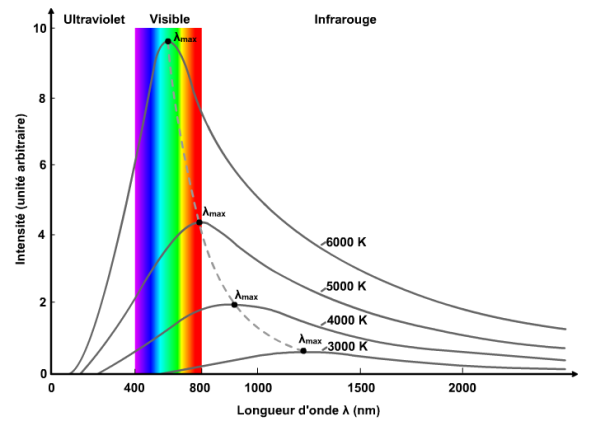
Un corps noir est un modèle physique.

C'est un corps dont le spectre d'émission électromagnétique ne dépend que de sa température.
L'intensité du rayonnement émis a un maximum pour une longueur d'onde de rayonnement qui ne dépend que de la température du corps.

Je n'aime pas ton dessin qui a du être tracé par un artiste et pas par un physicien tant il est imprécis.

En voila un autre moins imprécis.



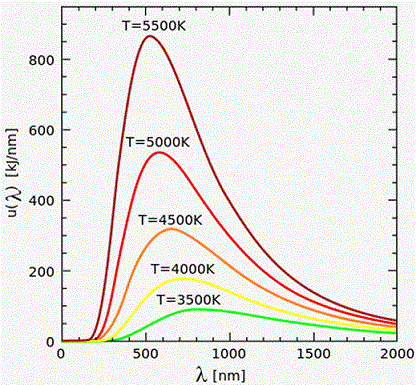
On voit par exemple sur le dessin, qu'un corps à une température de 5500 K a un spectre d'émission large, mais que l'intensité max à lieu a une longueur d'onde de environ 530 nm
Conforme a ce qui serait calculé par la loi de Wien : Lambda max = 2,898.10^-3/T
-----
Un corps noir est un modèle physique, donc pas un corps qui existe vraiment.

Mais les corps réels ont des propriétés assez proches du modèle appelé "corps noir"... Et on peut donc utiliser la théorie avec les corps réels aussi (en sachant qu'on fait de petites erreurs, mais pas très grandes).

Il y a une caractéristique (appelée émissivité) qui permet de "mesurer l'écart" entre un corps donné réel et le corps noir (qui n'est qu'un modèle). Mais ceci n'intervient pas dans le genre d'exercices proposés en Secondaire.








  

Bonsoir à tous, Cynthi97, je pense que tu parles d'un sujet de synthèse qui a été publié par le Ministère de l'éducation. je l'ai étudié et la définition d'un corps noir la plus adaptée pour ce sujet est " Objet idéal qui absorberait toute l'énergie électromagnétique qu'il recevrait, sans en réfléchir ni en transmettre, dont le spectre électromagnétique ne dépend que de sa température.". la loi de Wien est une formule qui (citée plus hauts par J-P) met en relation la température, la longueur d'onde max ( max) et une constante. Si mes souvenirs sont bons: dans le document1 du groupement (le texte qui parle des 2 physiciens ayant eu le prix Nobel pour la découverte du corps noir), il est stipulé que T= 3x10^3K (regarde dans le texte car je n'en suis pas encore sur). Tu fais donc le calcul: max= constante/T.
Cordialement, Zerb'

Bonsoir,
merci à tous de vos explications