Bonsoir, faisant un exercice de physique je pense avoir fait une erreur mais ne la trouve pas je viens donc demander de l'aide. Voici l'énoncé ( j'ai mis le schéma plus bas )
Soit un condensateur plan formé de deux armatures A1 et A2 reliées à un générateur. celui-ci produit entre ses deux armatures un champs électrostatique uniforme. La valeur du champs E vaut 4900 V.m^-1. Un électron pénètre entre les deux armatures en venant de la gauche à l'ordonnée y0 avec une vitesse v0.
1/ Rappeler l'expression de la force électrique Fe, qui s'exerce sur une particule de charge q présente dans un champ électrostatique E. Montrer qu'ici, le poids de l'électron est négligeable par rapport à la force électrostatique.

Ici je n'ai pas eu de problème
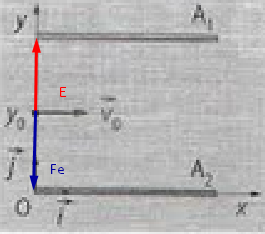
2/ Représenter sur la figure ( voir ci-dessous ) et sans soucis d'échelle, le vecteur champ électrique E ainsi que le vecteur Fe au point d'entrée de l'électron, si l'on veut que l'électron soit dévié vers le bas

Ici aussi je pense avoir réussi ( voir schéma )
3/ En déduire la valeur des coordonnées Ex et Ey du vecteur E
J'ai trouvé que Ex=0  et Ey=4900
4/ Quelle est l'armature chargée positivement ?
J'ai dis que c'était A1 car le vecteur Fe allez vers le bas alors que le vecteur allez vers le E
5/ Établir l'expression littérale des coordonnées ax et ay du vecteur accélération de l'électron dans le repère (O,x,y) en fonction de e, m et des coordonnées Ex et Ey du vecteur E en citant la loi utilisé
Ici j'ai utilisé la 2nde loi de Newton et j'ai dit que le poids été négligeable on obtient donc Fe= m*a
Donc q*E=m*a
a=(q*E)/m
Donc on obtient Ax=(-e*Ex)/m et Ay=(-e*Ey)/m
6/ En déduire les équations horaires du mouvement de l'électron
Ici j'ai trouvé que OM(x)= Vo*t et que OM(y)=((-e*Ey)/2m)*t²+Vo*t+Yo
Mais je pense m'être trompé en faisant des primitives donc je viens demandais confirmation
7/ Montrer que l'équation de la trajectoire de l'électron e st de la forme y= Ax²+B avec A et B des constantes qu'on expliquera. A quel type de trajectoire correspond-il?
Ici je suis bloqué étant donné que j'ai un doute sur la 6/

Je vous remercie d'avances pour vos réponses