A.N. :

Salut,

Epp + Ec = Em = 0,042 J

au point le plus haut (vitesse nulle) : Ec = 0 et donc Epp = Em = 0,042 J

mgL(1-cos(theta0)) = 0,042

0,236 * 9,8 * 0,41 * (1-cos(theta0)) = 0,042

1 - cos(theta0) = 0,044292

cos(theta0) = 0,955708

theta0 = arccos(0,955708) = 17° (arrondi)

Sauf distraction.  

Ce que j'ai écrit à 19:26 est faux ?

Bonjour,

Le calcul littéral est exact.
L'application numérique est fausse car E_ppmax = 0,042J et non 0,024J

Faute d'énoncé au niveau du schéma donc

Ton " énoncé " n'est pas des plus clairs, on ne sait pas trop quelle longueur est représentée en abscisse, mais il semble évident que la courbe 1 représente l'énergie mécanique, laquelle reste constante en l'absence de frottements.

Quand l'énergie potentielle est maximale, l'énergie cinétique est nulle donc cette énergie potentielle maximale est égale à l'énergie mécanique soit 0,042 J comme on peut le constater sur ton schéma.

Par calcul, on montre que x(m) est l'abscisse du point massique mobile. (origine au point de repos ...)

La courbe 1 est l'EPP du mobile (avec référence des altitudes au point bas de la trajectoire)
La courbe 2 est l'Energie cinétique.
La courbe 3 est l'énergie mécanique du système.

Le dessin n'est pas complet puisque on ne voit pas les points à vitesse nulle.
C'est probablement fait exprès pour pousser à calculer via les énergies et pas juste "lire sur le dessin".

Voici, le dessin complété (pour toute la trajectoire).



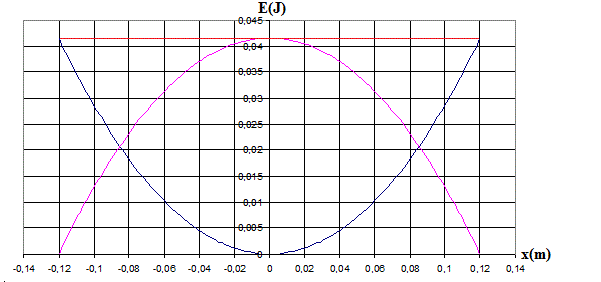
Mais si on a cela, on a directement 0,12 = 0,41*sin(alpha max)

alpha max = 17° (arrondi)

D'accord, j'ai compris.

Justifier à quoi correspond les courbes.

Courbe 1 : Em car Em=0.
Courbe 2 : Ec=1/2mv² quand v augmente Ec augmente
Courbe 3 : Epp=mgz quand z augmente Epp augmente

ça suffit ?

J'ai mal repéré  les courbes dans mon message précédent.

La courbe 3 est l'EPP du mobile (avec référence des altitudes au point bas de la trajectoire)
La courbe 2 est l'Energie cinétique.
La courbe 1 est l'énergie mécanique du système.

Mon message de 18h34 est juste ?