Inscription / Connexion Nouveau Sujet
Les Forces
Bonjour,
J'ai un DM de physique à faire pour la rentrée et j'ai quelques petits problèmes.
J'ai regardé un peu sur le forum avant de poster ce message, car même si plusieurs Topics abordent le sujet ils ne répondent pas vraiment à ce que je ne comprends pas.
Voici l'énoncé :
Un skieur remonte à téléski une pente inclinée d'un angle 
=14,5° par rapport à l'horizontale.
La perche du téléski fait un angle 
=45° avec la pente.
Le mouvement du skieur de masse m=90kg est une translation rectiligne uniforme.
On néglige la résistance de l'air et les frottements entre la neige et les skis.
g=9,8 N.kg-1. Le mouvement du skieur est étudié dans le référentiel terrestre supposé être galiléen.
1) Faire le Bilan des forces exercées sur le skieur.
2) Quelle loi s'applique sur le skieur. En déduire une relation entre les forces.
3) Représenter ces forces sur un schéma sans souci d'échelle et en appliquant toutes les forces au centre d'inertie du skieur.
4) Déterminer les coordonnées de chaque vecteur dans le système (O,x,y)
5) Projetez la relation obtenue à la question 3) sur l'axe Ox et déterminer la valeur de
6) Projeter la relation obtenue à la question 3) sur l'axe Oy et déterminer la valeur de
7) Donner les caractéristiques de la force exercée par le skieur sur la piste.
8) Refaire un schéma à l'échelle 1 cm pour 200N en respectant les valeurs des angles et vérifier que 
=
Je vous mets ce que j'ai réussi à trouver en sachant que si vous trouvez qu'il faut que je rajoute des choses, dites le moi :
1) Bilan des forces exercées sur le skieur :
-Le Poids
-La réaction de la pente
-La tension de la perche
2) La loi qui s'applique au skieur est le principe d'inertie car le skieur a un mouvement rectiligne uniforme dans un reférentiel galiléen.
Donc : +
+
=
[Je ne suis pas sûre de la relation]
4) Je ne vois pas comment on fait
A partir de là je bloque.
Pouvez-vous m'aider?
Merci d'avance
Voici le schéma
Ah oui! Oups
Donc : Ty = Rcos
Et Tx = T
C'est bon?
Pour la suite après je vois toujours pas comment on fait 
Ok merci beaucoup.
Et donc après pour calculer la valeur de et
je vois pas non plus comment faire.
Désolée de vous déranger 
pour Ox : prends la composante de chaque force suivant cet axe et sachant que le mouvement est rectiligne et uniforme , la somme des forces est nulle donc la somme de ces composantes est nulle. => Tu peux en déduire \vec{T}
pour Oy : meme raisonnement... => Tu peux en déduire \vec{R_n}
3)
-----
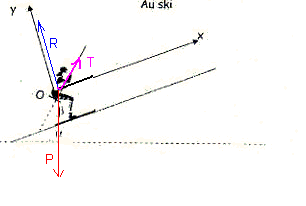
4)
vecteur T (|T|.cos(beta) ; |T|.sin(beta))
Vecteur R (0 ; |R|)
vecteur P (-|P|.sin(alpha) ; -|P|.cos(alpha))
-----
5 et 6)
T.cos(beta) - P.sin(alpha) = 0
T.sin(beta) + R - P.cos(alpha) = 0
T.cos(45°) - 90*9,8.sin(14,5°) = 0
T.sin(45°) + R - 90*9,8.cos(14,5°) = 0
T = 90*9,8.sin(14,5°)/cos(45°) = 312 N
T.sin(45°) + R - 90*9,8.cos(14,5°) = 0
312.sin(45°) + R - 90*9,8.cos(14,5°) = 0
R = 633 N
-----
Sauf distraction. 
Ok jd crois avoir compris.
Donc je fais :
Px + Rx + Tx = 0
-Psin + 0 + Tcos = 0
Donc Tcos = Psin
Et
Py + Ry + TY = 0
-Pcos + R + Tsin = 0
P=-R donc:
-Pcos - P + Tsin =0
Tsin = Pcos +P
C'est ça!? Ou alors je fais n'importe quoi 
P=-R ?? non ils n'ont pas la meme direction !!
il suffit juste de reprendre la valeur de T pour calculer Rn...
Annuler
connectez vous