Inscription / Connexion Nouveau Sujet
Le travail d'une force et les puissances.
Bonjour,
J'ai un devoir maison à faire, mais malheureusement, il y a quelques questions que je n'arrive pas à faire. J'ai déjà, de multiples fois regardé dans mon cours mais cela ne m'a en rien aidé. Je vous présente ainsi le sujet et les questions ( que j'ai faîtes ou non)
A) Un skieur de masse m=90kg est tiré sur une distance de d=500 m par un remonte-pente à vitesse constante v=5.0 m/s. Son mouvement est rectiligne le long de la piste incliné d'un angle (alpha)=30°par rapport à l'horizontale. La perche exerce une force constante de valeur T dont la direction fait un angle B = 40° par rapport à la piste. Les forces de frottements sont équivalents à une force unique de valeur Ft = 50N.
1)Faire un schéma de la situation. Nommer les actions exercées par le skieur et tracer les vecteurs force. Je l'ai déjà réalisé, et je pense que c'est correct.
2)Déterminez les valeurs des forces qui ne sont pas données dans l'énoncé. Expliquer et rédiger la réponse. Cette question-ci me pose quelques problèmes. J'ai répondu ainsi : la réaction du support n'est pas donné or la force est perpendiculaire au mouvement tout au long du déplacement donc R= 0
La force de traction F du remonte-pente : T*cos(alpha)=Ft soit T= 50/cos(40) = 65 N
je ne suis absolument pas sur de ma réponse :s
3)Calculer le travail de chacune des forces. Préciser si le travail est moteur ou résistant. Mes formules sont justes, je pense du moins mais mes résultats me paraissent incohérant par rapport à la question qui va suivre ci dessous.
Wab(P)= P*AB*cos(p;ab)
= 90*9.81*500*cos(120)
= - 220725 J ( le travail est résistant)
Wab(T)=T*AB*cos(t;AB)
=65*500*cos(40)
=24896 J(le travail est moteur)
Wab(Ft)=Ft*AB*cos(Ft;AB)
= 50*500*(cos(180)) car les frottements sont colinéaires mais de sens opposé au mouvement)
= -Ft*AB
= -50*500
= -25000J(le travail est résistant)
4) Calculer la somme des travaux. Commenter
Cette question me pose problèmes puisque la somme de mes travaux me fait un résultat négatif donc une somme de travaux résistante. Je ne pense pas que cela puisse être possible mais malheureusement je ne trouve pas mon erreur.
B) Arrivé en haut de la piste, le skieur s'élance tout schuss dans la piste plane inclinée d'un angle x'=40° avec l'horizontale. Au milieu de la piste deux cellules chronométriques séparées de 50 m permettent de déterminer la vitesse instantanée atteint par le skieur à cet endroit. La vitesse limite du skieur est de 216km/h. L'ensemble des forces de frottements qui s'exercent sur le skieur a une valeur F'.
5)Faire un schéma. (Déjà réalisée aussi) Déterminer le travail du poids sur les 50m séparant les deux cellules. Ma réponse est celle-ci : Wab(P)=m*g*AB*cos(p;AB)
=90*9.81*50*cos(40)
=33817 J
6) En déduire le travail de la force de frottement par un raisonnement complet et claire. J'ai répondu On sait que la vitesse entre les deux cellules est constante donc la somme vectorielle est nul ( poids+réaction du support+frottements ... d'apres la 1 er lois de Newton)
Or la force de frottement est contraire à celle du poids ( force exercé par le skieur )
Wab(P)= -Wab(F)
7)Déterminer la valeur de la force de frottement. D'après la question 6) Wab(P)=-Wab(F)
Donc Wab(F)= -33817 J
8) Déterminer la puissance moyenne de la force de frottement entre les deux cellules. J'ai ainsi répondu, pour finir, P=W/Δt P= -33817 / 3600
P= -9.4 W Le problème s'est que je ne suis pas sur qu'une puissance puisse être négative et je ne pense pas que mon résultat soit exact.
Pourriez-vous m'aider à comprendre comment faire s'il vous plaît.
Je vous remercie d'avance 
Bonjour,
Bienvenue sur l'  pour ton premier problème !
pour ton premier problème !
____________
Question 1
L'idéal serait que tu puisses poster un schéma.
Sinon, il faut que tu expliques très bien
Il me semble qu'il y a 4 forces à identifier ; il sera nécessaire de projeter sur des axes parallèle et perpendiculaire à la piste pour trouver les différentes composantes de ces forces et pour faire les calculs.
Quelles sont ces 4 forces ?

Mes 4 forces sont le poids, la réaction du support, les frottements et la force de traction exercé par le remonte-pente.
Très bien !
Quelle est l'intensité du poids ?
Toutes les forces doivent être projetées sur les axes parallèle et perpendiculaire à la piste.
Quelles sont (littéralement) :
. toutes les composantes parallèles à la piste
. toutes les composantes perpendiculaires à la piste ?

Pour l'intensité du poids la formule si je me souviens bien c'est P= M*g c'est bien cela ?
Pour le reste alors : le vecteur poids est suivant l'axe du skieur dirigé vers le bas( vers la piste). La réaction du support est "identique" par rapport au vecteur poids seulement celui-ci n'est plus dirigé vers le bas mais à présent dirigé vers le haut. La composante des frottements elle est parallèle à la piste dirigé dans le sens contraire du déplacement du skieur. Pour finir, la composante du remonte-pente (elle a été réaliser grâce à des projections avec l'axe y parallèle à la piste et x perpendiculaire à celle-ci) est dirigé dans le sens même du mouvement.
Je ne sais pas si je suis assez claire (désolé) :s
C'est pas mal ; mais il me semble qu'il y a quelques inexactitudes.
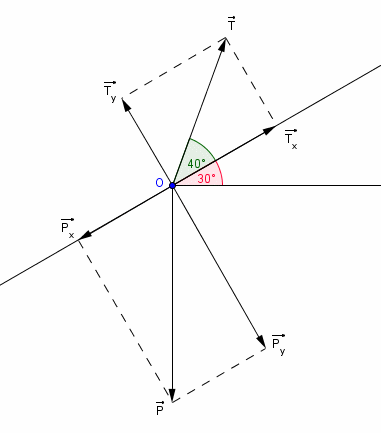
Voilà une image sur laquelle ne figurent que deux forces, le poids et la traction ; ces deux forces sont décomposées selon les axes dont je t'ai déjà parlé à deux reprises.
Oui, le poids c'est
Quelle est donc l'intensité (la valeur, la norme...) du poids ?
Et que valent les composantes du poids sur les axes ?
Les deux forces qui ne sont pas sur mon schéma sont :
. la force de frottement
. la réaction normale à la piste
Leurs directions sont telles qu'il est très facile de les projeter (elles se projettent en vraie grandeur).

L'intensité du poids est donc p=m*g soit p= 90*9.81
= 882.9 N
La somme des composantes ( d'après la première lois de Newton ) sont nulle puisque: dans un référentiel galiléen, le centre d'inertie G d'un solide soumis à un ensemble de forces dont la somme vectorielle est nulle est soit au repos, soit animé d'un mouvement rectiligne et uniforme (le vecteur vitesse demeure constant). Or dans l'énoncé on nous indique bien que la vitesse est constante à v= 5m/s
Très bien !
Oui l'intensité du poids est environ 883 N
L'égalité vectorielle indispensable et essentielle pour ce problème est bien :
Et en projetant cette égalité sur les axes (en prenant les composantes) tu vas pouvoir déterminer petit à petit toutes les valeurs inconnues. Il faut s'y prendre dans le bon ordre.
Que valent les intensités Px et Py ?
Que vaut la projection de la force de frottement sur l'axe Ox ?

je vois pas trop comment faire pour trouver ces intensités.  On m'a déja dis que -Wab (F) = Wab(P) mais je pense pas que cela répond à la question. Il faut utiliser l'égalité vectorielle mais je vois pas comment faire...
On m'a déja dis que -Wab (F) = Wab(P) mais je pense pas que cela répond à la question. Il faut utiliser l'égalité vectorielle mais je vois pas comment faire...
On n'en est pas encore à s'occuper des travaux. Il faut tout d'abord trouver les intensités de toutes les forces.
Comment faire ? Un tout petit peu de trigonométrie...

Eh bien comme on sait l'intensité du poids, on peut tout simplement faire px= 883 * sin ( alpha) et Py= 883* cos (alpha)
= 883* sin (30) Py=883* cos (30)
Je suis pas du tout sûr !
C'est tout à fait cela !
Tu peux chercher les valeurs approchées correspondantes.
Considère ensuite l'axe Ox (parallèle à la piste) :
trois composantes :
. Px
. F
. Tx
Deux vers le bas et une vers le haut.
La somme des trois est nulle
Que vaut Tx ?

Px =441.5 N et on connaît F d'après l'énoncé vaut 50 N
on additionne cela fait 491.5 et comme la somme vectorielle est nulle donc Tx = -491.5 N c'est cela?
C'est exactement cela !
Maintenant que tu connais Tx, tu peux en déduire la valeur de T (encore un peu de trigonométrie...)

Oui.
T = Tx / cos(40°)
Ceci te permet de calculer la valeur de T
D'où tu pourras déduire la valeur de Ty (eh oui, encore de la trigonométrie...  )
)
Alors tu considéreras l'axe Oy (axe perpendiculaire à la piste) ; trois composantes :
. Py vers le bas
. Ty vers le haut
. R, réaction du "support", c'est-à-dire réaction normale de la piste, vers le haut
Et la somme de ces trois composantes est nulle. Donc... cela te permet de calculer la valeur de R
Ainsi sera terminée la deuxième question.
Nous traiterons des travaux et des puissances demain, car je vais m'arrêter pour ce soir (mais il se peut aussi que quelqu'un t'aide ce soir et cette nuit, même si je pense que la nuit est faite pour dormir)

La valeur que tu indiques à 21 h 50 ; oui, mais pourquoi ce signe "moins" ?
La norme d'un vecteur est toujours positive.
Les composantes sur les axes ont un signe qui dépend de l'orientation de l'axe.


Relis la différence entre :
. la norme (toujours positive) d'un vecteur
. et une composante de ce vecteur sur un axe  qui vaut le produit scalaire
qui vaut le produit scalaire et qui peut en conséquence être positive ou négative.

En orientant l'axe Ox, parallèle à la piste, vers le haut, c'est-à-dire aussi dans le sens du mouvement
et l'axe Oy également vers le haut (vers le ciel...) :
Le poids a pour norme
 883 N
883 N
les composantes du poids :
. sur l'axe Ox  - 441 N
- 441 N
. sur l'axe Oy  - 765 N
- 765 N
La force de frottement a pour norme 50 N
les composantes de cette force :
. sur l'axe Ox = - 50 N
. sur l'axe Oy = 0 N
La force de traction
. a une composante sur l'axe Ox qui vaut  491 N
491 N
donc sa norme vaut  642 N
642 N
. et sa composante sur l'axe Oy vaut donc  412 N
412 N
Quelle est la norme de la réaction normale du sol ?

on fait la somme vectoriel de ces 3 normes puisqu'on s'est qu'elles sont au final nul et on en déduis que R=191 N. C'est çela? :s
Pour la norme, je suis tout à fait d'accord mais d'après les calculs que j'ai effectué cela me met un résultat négatif pourquoi?
Sur l'axe Oy trois composantes :
. Py  - 765 N
- 765 N
. Ty  412 N
412 N
. R inconnue
La somme vectorielle
et donc sa projection sur tout axe est nulle également
Py + Ty + R = 0
Que vaut R ?

Oui,
Tu as des problèmes avec les signes...
_____________
On peut passer aux questions 3 et 4
Un travail moteur (la force ou la composante de force dans le sens du mouvement) est compté positivement
Un travail résistant (la force ou la composante de force en sens inverse du mouvement) est compté négativement
J'ai orienté l'axe Ox dans le sens du mouvement (vers le haut de la piste)
Les forces ou les composantes de force perpendiculaires au mouvement effectuent un travail nul.

pour les signes, je me rappelais plus mais ça m'a permis de revoir merci 
Pour les questions 3 et 4.
Donc WAB (R) est nul puisqu'il est perpendiculaire tout au long du mouvement, et le travail du poids et des frottements sont donc nul. Le travail T lui est moteur.
pardon pour le travail du poids et des frottements c'est résistant donc négatif petite erreur d'inatention :s
Exact, après la rectification.
____________
Deux manières pour calculer :
ou bien WAB =
Ou bien, si l'on a projeté la force sur l'axe AB orienté de A vers B pour trouver la composante Fx et comme Fx = F.cos(
 ) alors
) alors
WAB = Fx  AB
AB
Au choix !

pour le poids j'ai fais comme dans l'énoncé. Pour T je rectifie puisque c'était faux donc
Wab(T)= T*AB*cos(T;AB)
= 642*500*cos(40)
= 245900.3 J (travail moteur)
pour la force de frottement je pense que dans l'énoncé c'est aussi bon et pour la réaction du support j'hésite puisqu'on a dit que le travail de R était nul car il était perpendiculaire au mouvement c'est exact?
Oui, si l'on n'arrondit pas la valeur de la force de traction on trouve un travail de cette force égal à 245 725 J
WAB(T) = [(90  9,81
9,81  0,5) + 50 ]
0,5) + 50 ]  500
500  cos(40°) / cos(40°) = 245 725 joules
cos(40°) / cos(40°) = 245 725 joules
Comme quoi, c'est plus facile avec les composantes !
Bien sûr la réaction normale (c'est-à-dire perpendiculaire) du support a un travail nul.

merci mais est-ce que tu pourrais m'aider pour la question 6) parce que celle-là me pose problème bien sur si tu as du temps à m'accorder parce que tu m'as deja bien aidé. Je te remercie.
Partie B :
Question 5
Tu as une erreur. L'angle de 40° est l'angle entre la piste et l'horizontale. Or pour calculer le travail du poids (qui est une force verticale) il faut utiliser l'angle entre la piste et la verticale... c'est-à-dire 50°
Question 6
Parfait. Cela me conviendrait tout à fait !
Question 7
Tu ne réponds pas à la question.
Après avoir corrigé la valeur du travail (nouvelle réponse à la question 5) il faut calculer la valeur de la force (tu as le travail et cette force de frottement a même direction, mais sens opposé, au déplacement).
Question 8
Pour calculer la puissance d'une force dont tu connais le travail mais pas la valeur il faut savoir quelle durée a été nécessaire pour le travail.
Que vaut la vitesse en mètres par seconde ?
Quelle est la durée (en secondes) nécessaire pour franchir 50 m à cette vitesse ?
Il est probable que je ne pourrai pas lire ta réponse avant cet après-midi.
Bon courage ! Tu as bien travaillé (et je pense que tu as progressé).

Pour JULIA61
comment tu trouves les valeurs des cos ci dessous (120) (40) et (180) ?? je bloque que sur ca j etudie la physique en autodidacte et des fois je bloque sur des trucs cons !
merci
P*AB*cos(p;ab)
= 90*9.81*500*cos(120)
Wab(T)=T*AB*cos(t;AB)
=65*500*cos(40)
Wab(Ft)=Ft*AB*cos(Ft;AB)
= 50*500*(cos(180))
A) Un skieur de masse m=90kg est tiré sur une distance de d=500 m par un remonte-pente à vitesse constante v=5.0 m/s. Son mouvement est rectiligne le long de la piste incliné d'un angle (alpha)=30°par rapport à l'horizontale. La perche exerce une force constante de valeur T dont la direction fait un angle B = 40° par rapport à la piste. Les forces de frottements sont équivalents à une force unique de valeur Ft = 50N.
1)Faire un schéma de la situation. Nommer les actions exercées par le skieur et tracer les vecteurs force. Je l'ai déjà réalisé, et je pense que c'est correct.
2)Déterminez les valeurs des forces qui ne sont pas données dans l'énoncé. Expliquer et rédiger la réponse. Cette question-ci me pose quelques problèmes. J'ai répondu ainsi : la réaction du support n'est pas donné or la force est perpendiculaire au mouvement tout au long du déplacement donc R= 0
La force de traction F du remonte-pente : T*cos(alpha)=Ft soit T= 50/cos(40) = 65 N
je ne suis absolument pas sur de ma réponse :s
3)Calculer le travail de chacune des forces. Préciser si le travail est moteur ou résistant. Mes formules sont justes, je pense du moins mais mes résultats me paraissent incohérant par rapport à la question qui va suivre ci dessous.
Wab(P)= P*AB*cos(p;ab)
= 90*9.81*500*cos(120)
= - 220725 J ( le travail est résistant)
Wab(T)=T*AB*cos(t;AB)
=65*500*cos(40)
=24896 J(le travail est moteur)
Wab(Ft)=Ft*AB*cos(Ft;AB)
= 50*500*(cos(180)) car les frottements sont colinéaires mais de sens opposé au mouvement)
= -Ft*AB
= -50*500
= -25000J(le travail est résistant)


