Inscription / Connexion Nouveau Sujet
Le travail d'une force
Bonjour,
J'ai un DM de Maths à effectuer et je bloque sur l'un des exercices qui concerne aussi la physique. Je suis en 1ère spé maths.
Enoncé:
Lorsqu'un objet se déplace, la force qui s'applique sur cet objet "produit un travail" c'est a dire de l'énergie. Les expériences physiques montrent que ce travail, noté W, s'exprime par: W=F.AB (vecteurs), où F (vecteur) est la force (supposés constante) qui s' applique sur l'objet matériel et AB (vecteur) correspond au déplacement (supposé rectiligne) de A à B.
Si la force est exprimé en Newton et la longueur AB en mètre, le travail W est en Joule.
Une skieuse pesant 55kg utilise un remonte-pente d'une longueur AB=800m.
L'inclination de la pente est de 30°.
a) Exprimer le travail W du poids P de la skieuse lorsqu'elle passe de A à B.
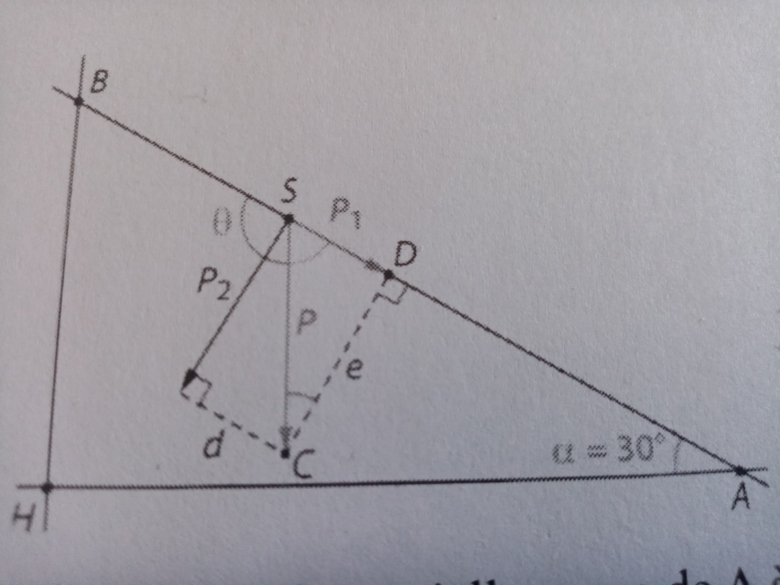
On a écrit P = P₁ + P₂ où P₁ est colinéaire au vecteur AB et P₂ lui est orthogonal
b) justifier que l'angle CSD = 60° et en déduire la valeur de l'angle θ = (AB,P)
c) calculer W
d) comment expliquer que W est négatif ?
e) quelle énergie doit fournir le remonte pente pour tracter la skieuse de A à B ?
f) Quel est le travail fourni par P2 au cours du déplacement de A à B?
g) démontrer que l'on a aussi : W= P.HB=P₁ .AB. Que représente la longueur HB ?
J'ai répondu à la première question, j'ai trouvé:
W=P.AB= IIPII * IIABII * cos (P,AB)
Ces lettres représentent des vecteurs (je ne sais pas comment on met la flèche). Les 2 barres représentent la norme.
modération> **pour être honnête, on va plutôt dire que c'est le résultat mis par un aidant côté maths avant que ton sujet y soit verrouillé**
Pour CSD c'est un triangle rectangle donc 90+30+60=180 puis angles alternés internes et donc thêta = 120.
Bonjour,
L'angle entre les vecteurs et
est égal à 120°
= 55 * 9,81 * 800 * cos (120°) = -215800 J
Ce travail est négatif car le poids est ici une force résistante.
****citation inutile supprimée****
Merci beaucoup, pourriez-vous m'aider également aux questions restantes?
J'ai trouvé par la e) que le remonte pente doit fournir l'énergie potentielle égale à 215800 J
Pour la f) j'ai trouvé que le travail fourni par P2 est nul car ce vecteur est perpendiculaire à la trajectoire
Question e) :
Si le remonte pente tracte la skieuse à vitesse constante et si tous les frottements sont négligés alors l'énergie fournie est opposée au travail du poids et est égale à 215800 J
Question f) :
Ta réponse est exacte.
Question e) :
Si le remonte pente tracte la skieuse à vitesse constante et si tous les frottements sont négligés alors l'énergie fournie est opposée au travail du poids et est égale à 215800 J
Question f) :
Ta réponse est exacte.
Merci beaucoup!!
Le travail du poids est égale à la somme des travaux des forces et
Or le travail de est nul
Il en résulte que le travail de est égal à celui de
Je te laisse calculer ce travail et montrer qu'il est égal à - P * HB à condition de rectifier la figure de manière que HB soit perpendiculaire à AH
Le travail du poids est égale à la somme des travaux des forces
Or le travail de
Il en résulte que le travail de
Je te laisse calculer ce travail et montrer qu'il est égal à - P * HB à condition de rectifier la figure de manière que HB soit perpendiculaire à AH
Je n'ai pas compris comment je peux procéder, je n'ai pas la longueur de HB.
Bonjour
odbugt1 utilise l'écriture Ltx
tu peux voir ici : ![]() [lien]
[lien]
tu peux aussi utiliser l'éditeur Ltx (Ltx avec les 3 petits points rouges sous ta zone d'écriture )
pour écrire tu écris \vec u entre les balises [ tex][ /tex]

C'est bon !
Maintenant tu exprimes P1 en fonction de P et de α puis tu reportes le résultat obtenu dans W = - P1 * AB
C'est bon !
Maintenant tu exprimes P1 en fonction de P et de α puis tu reportes le résultat obtenu dans W = - P1 * AB
Je n'ai pas compris ce qu'il faut que je fasse
P= m*g= 55*9,81= 539,55
Nous avons sin α = P1 / P
sin 30= P1 / 539,55
Donc P1 = 539,55 * sin 30 = 269,775
W= -P1 * AB = -539,55 * 800 = -215 820
Je viens de faire la suite et j'ai trouvé que HB vaut 400m
Donc W= -P*HB= -539,55*400= -215 820
Nous avons donc démontré W= P.HB=P₁ .AB (en vecteurs)
Pour finir, la question, HB représente l'altitude d'arrivée de la skieuse.
Voilà j'ai fini, je pense avoir juste. Je vous remercie énormément pour votre aide.
Ce qui est bien : sin(α) = P1 / P 
Ce qui est inutile car non demandé : Tout le reste
Ce que tu aurais du faire à partir de sin(α) = P1 / P :
Exprimer P1 en fonction de P et de α : P1 = .......... et reporter le résultat dans W = -P1 * AB
C'est à dire tenir compte de mon post du 18-04-22 à 18:37
( ! ) Aucun calcul numérique n'est demandé.
Ce qui est bien : sin(α) = P1 / P

Ce qui est inutile car non demandé : Tout le reste
Ce que tu aurais du faire à partir de sin(α) = P1 / P :
Exprimer P1 en fonction de P et de α : P1 = .......... et reporter le résultat dans W = -P1 * AB
C'est à dire tenir compte de mon post du 18-04-22 à 18:37
( ! ) Aucun calcul numérique n'est demandé.
Cela me donne donc W=-(P*sin α) * AB
Et aussi W = -P* sin α * AB
Parfait !
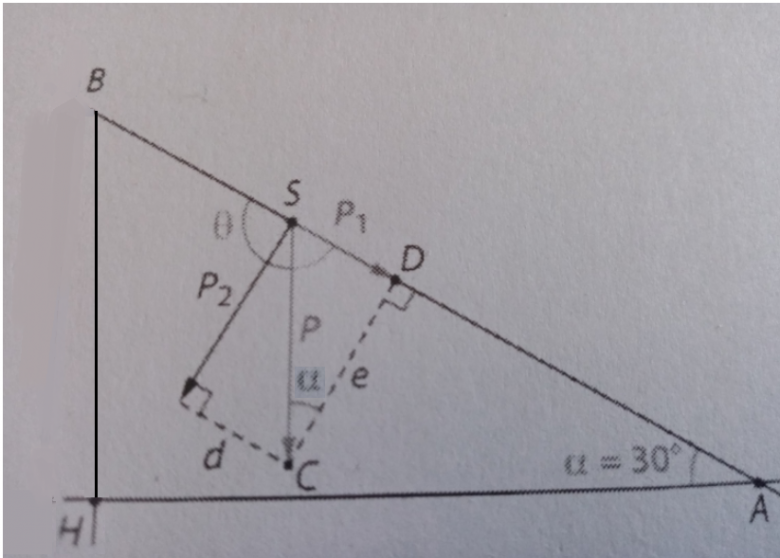
Et maintenant pour terminer regarde mon schéma (18-04-22 à 18:53)
A quoi est égal AB * sin α ?
Encore de la trigonométrie de collège ! ! !
Et aussi W = -P* sin α * AB
Parfait !
Et maintenant pour terminer regarde mon schéma (18-04-22 à 18:53)
A quoi est égal AB * sin α ?
Encore de la trigonométrie de collège ! ! !
C'est égal à la hauteur HB, l'altitude d'arrivée de la skieuse
C'est égal à la hauteur HB, l'altitude d'arrivée de la skieuse
Oui
Donc W = - P * HB
C'est justement ce qu'on te demandait de démontrer ( au signe près ) à la question g)

 ) sur l'île de la physique. Je savais que tu y trouverais toute l'aide attendue sur ce type d'exercice.
) sur l'île de la physique. Je savais que tu y trouverais toute l'aide attendue sur ce type d'exercice. 

