Inscription / Connexion Nouveau Sujet
La Momie - Datation
Bonjour j'au besoin d'aide en datation
Énoncé :
Une momie a été découverte en Égypte. On réalise une datation au C 14. On observe une diminution de 40% de la proportion en C14 de la momie.
1) Pourquoi le carbone 14 n'est-il plus renouvelé à partir du décès des etres vivants ?
Réponse proposée : Il n'est plus renouvelé car la matière organique disparait, à la mort d'un organisme vivant, tout échange avec le milieu extérieur cesse, de sorte que le carbone 14 n'est plus renouvelé : le nombre d'atomes de carbone 14 contenus dans les restes de l'organisme se met donc à diminuer progressivement, au rythme de la décroissance radioactive.
2) il faut dater la momie (plus tard)
3) Peut-on utiliser la methode de datation au carbone 14 pour dater des dinosaures qui se sont eteints il ya 65.5 milions d'années ? Pourquoi ?
Réponse : On ne peut pas l'utiliser car le décès date de trop longtemps, la proportion de C14 est devenue nulle.
Pourriez vous me corriger ? M'aider ?
Bonjour,
1. TB
2. Tu n'as pas écrit la question
3. Quelle est la demi-vie du carbone 14 ? Quand les dinosaure ont-ils disparu ?

3) Elle est d'environ 3700 ans.
Rp: Les dinosaures ont disparu il y'a trop longtemps, il ya plus de 3700 ans
(Je ne vois pas trop où en venir  )
)
Merci pour ta réponse
Bonjour ,
Oui , c'est bon , vous avez répondu à 3 . La période de 14C est inadaptée pour ce trop long temps écoulé .
Rebonjour,
le prof m'a mis 11,5/20 pour cet exercice. J'aimerais savoir pourquoi, sachant que cette note compte au bac avec la réforme.
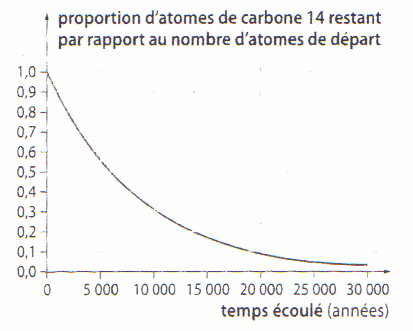
Pour la question 2, voici le graphique de la décroissance radioactive de la momie :
Et pour la question 2, j'ai répondu que d'après la courbe de décr.radioact., on peut en déduire que la momie date de 5000 ans...
Merci 
Re ,
Sur la courbe de décroissance du 14C , vous pouvez lire 2 choses :
1 - la valeur de la demi-vie ( ou période ) , c'est quand la moitié du nombre initial est restant ( ou que la moitié a disparu ) : donc pour 0.5 , je lis plus de 5000 ans .
En fait , on prend souvent la valeur de 5730 ans pour la 1/2 vie .
2 - Attention à l'énoncé : une diminution de 40% , veut dire qu'il reste 60% .
Donc , pour 0.6 , je lis moins de 5000 ans , plutôt vers 4000 ans .
Le calcul rigoureux utilisant la loi exponentielle donne 4223 ans .


