Inscription / Connexion Nouveau Sujet
la lunette astronomique
Bonjour à tous, quelqu'un aurait-il l'aimabilité de m'aider a répondre aux questions suivantes ?
On modélise une lunette astronomique afocale par deux lentilles minces convergentes L1 et L2 de distances focales respectives f'1= (50,0 ± 0,1) cm et f'2 = (5,0 ± 0,1) cm
On dispose aussi d'une troisième lentille mince convergente L3 de distance focale f'3 = (20,0 ± 0,1) cm et d'un écran afin de modéliser un il.
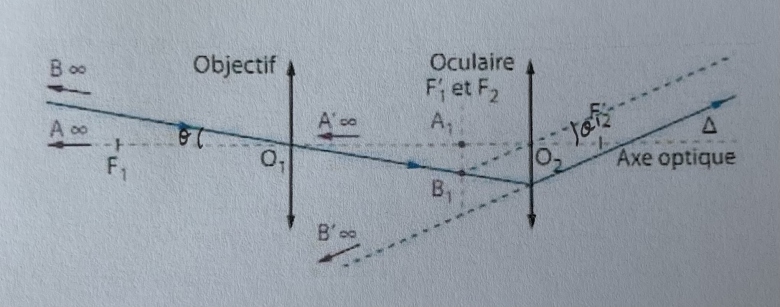
On souhaite observer, à l'aide de la lunette un bâtiment A(alpha) B(alpha) supposé à l'infini et vu à l'oeil nu sous l'angle (voir schéma).
Info : (± 0,1) cm signifie que l'incertitude-type sur la valeur de f vaut 0,1 cm, on aurait pu noter
aussi u(f') = 0,1cm
Info: L'il est représenté par une lentille qui modélise le cristallin, et un écran qui modélise la rétine.
L'écran est situé dans le plan focal de la lentille, en effet pour un objet à l'infini, l'image se forme sur la rétine.
1)Le grossissement d'une lunette s'écrit G = teta'/teta
a) Définir teta et teta'
b) Faites figurer teta et teta' sur le schema.
2) Remplacer la lunette par le modèle de l'il réduit (donc la lentille L3 + l'écran situé dans son plan focal).
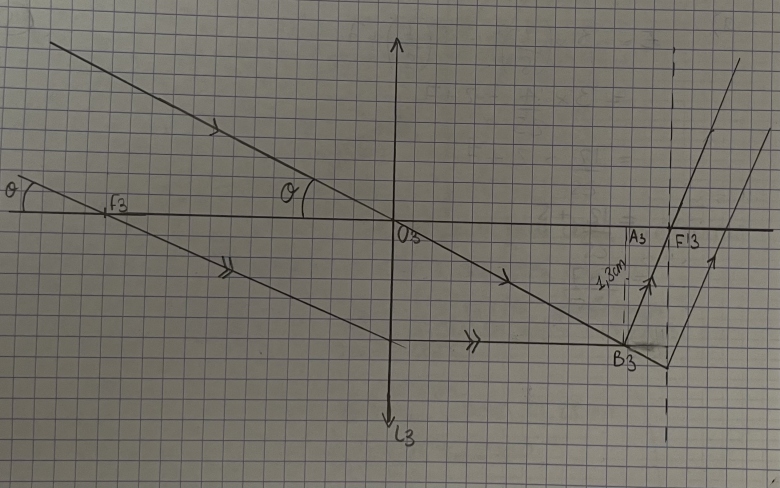
a) Faire un schéma et construire, sans souci d'échelle, l'image A3 B3 de l'objet A(alpha) B(alpha) supposé à l'infini par la lentille L3.
b) Où retrouve-t-on l'angle teta ? Le faire figurer sur la construction.
c) Exprimer puis calculer teta en fonction de f'3 et A3 B3, sachant que l'on mesure sur l'écran
A3 B3 = 1,3 cm.
3) On place maintenant le modèle de l'il réduit derrière la lunette astronomique afocale (on modélise ainsi un il qui regarde dans la lunette).
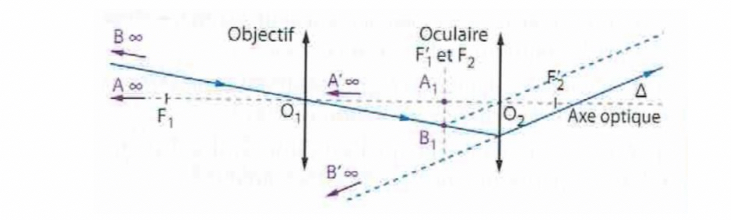
a) Que représente A'(alpha) B'(alpha) pour la lentille L3?
b) Construire, sans souci d'échelle, l'image A'3B'3 de A'(alpha) B'(alpha) par la lentille L3. Ou retrouve-t-on l'angle teta'? Faites le figurer sur la construction.
c) Calculer teta' sachant que l'on mesure sur l'écran A'3B'3 = 14,9 cm.
4) Calculer à partir des résultats précédents le grossissement expérimental de la lunette.
5)
a) Exprimer le grossissement Gthéorique à partir de f1' et f2' et calculer sa valeur.
b) Évaluer l'incertitude type u(G) = G(théorique)* √(((u(f'1))/(f'1))^2+(((u(f'2))/(f'2))^2
c) Réaliser ensuite le test de Student z = (|G(théorique)-G(expérimental)|) / u(G)
D'après la table de Student, si z < 2, la valeur mesurée est compatible avec celle attendue
Si z > 2 alors l'écart est trop grand pour assimiler la valeur mesurée à celle attendue. Conclure pour votre cas
J'ai déjà répondu à la 1) a) avec G=10cm
et b) avec teta a O1 et teta' a O2
Bonjour
Pour le grossissement : la valeur est correcte mais attention : G est un rapport de deux grandeurs de même nature donc : pas d'unité !
Pour b) si tu pouvais compléter ton schéma en y indiquant les angles demandés , le scanner puis le poster ici.
Pour la suite, il faut aussi faire un schéma précis et le poster ici.
OK pour les angles  et
et  '.
'.
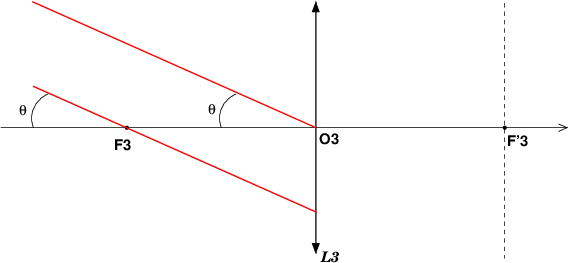
Pour la question suivante, il s'agit d'obtenir l'image A3B3 d'un objet AB situé à l'infini et vu de la lentille L3 sous l'angle  .
.
Le point A est situé à l'infini sur l'axe optique. Où est son image A3 par L3 ?
Le point B est à l'infini : il envoie sur L3 un ensemble de rayons parallèles entre eux, inclinés de l'angle  par rapport à l'axe optique. Où se forme son image B3 par L3 ?
par rapport à l'axe optique. Où se forme son image B3 par L3 ?
Je te laisse répondre aux questions et compléter la figure ci-dessous.
Tu n'y es pas du tout : relis bien l'énoncé :
Info: L'il est représenté par une lentille qui modélise le cristallin, et un écran qui modélise la rétine.
L'écran est situé dans le plan focal de la lentille, en effet pour un objet à l'infini, l'image se forme sur la rétine.
Tu dois savoir qu'une lentille donne d'un objet situé à l'infini une image située dans le plan focal image.