Bonjour kamikaz,

Que ce soit odbugt1 ou moi-même, nous t'avons maintes rappelé la nécessité de justifier ce que tu écris, ce qui n'est de nouveau pas le cas ici .

La physique-chimie ne se résume pas à des assertions ou à un enchaînement de formules non justifiées mais un raisonnement qui conduit à l'établissement d'un modèle jugée suffisant pour résoudre le problème posé (hypothèses, domaine d'études, précision, ...).

A noter que tu as une fiche de cours sur le sujet en cas de doute ici : Mouvement dans un champ de gravitation

La question est donc celle-ci : qu'est-ce qui t'a amené à ces résultats pour les questions 1 et 2.1.1. ?

Je ne souhaite pas revenir à ce qui s'est passé sur le dernier sujet, ce qui a conduit à une cacophonie générale : erreurs d'interprétation, confusions due à des retours différés ou non justifiés, etc.

D'après l'énoncé , le centre d'inertie du système est animé d'un mouvement circulaire uniforme.

Or mouvement circulaire est dit uniforme si la vitesse reste constante au cours du temps.
Vecteur vitesse
Le vecteur  vitesse est constant en norme mais pas en direction puisqu'il est tangent au cercle de la trajectoire durant tout le mouvement ( il est également orienté dans le sens de ce dernier).

D'où mes réponses aux questions 1) et 2)

Tu fais du hors sujet : je te rappelle la question posée par l'énoncé :

Ok , donc mes propositions sont fausses ..

Oui, parce que tu n'as pas pris le temps de lire attentivement la question posée. Ce sera primordial à faire le jour d'un examen : prendre le temps de lire de A à Z le sujet posé avant de commencer à y répondre.

Tu peux également reporter sur un brouillon les informations utiles, les notions de cours qui pourront de venir en aide pour chaque question posée, etc.

Pour en revenir sur cette question :

Ok ,

Système: le satellite

Referenciel: Référenciel géocentrique.

Bilan des forces: le poids P du satellite (mais je n'ai pas trouvé les autres forces)

Oups

Attention, tu attaques déjà la question suivante quand on est bloqué à la première ...

Ah d'accord ,

Donc on ne travaillera pas dans un référentiel géocentrique , mais dans un référentiel de Kepler.

Dans un mouvement circulaire , la vitesse est tangente à la trajectoire , la vitesse est constante en norme.

La dérivée du vecteur vitesse n'est pas nulle puisque sa direction change donc l'accélération est non nulle.
Le vecteur accélération pointe en permanence vers le centre du cercle ( l'accélération est dite centripète ) et posséde une valeur égale à :
a = v²/ R    
        
où v est la vitesse ( m.s^-1 )
      R est le rayon du cercle de la trajectoire (m)
       a est l'accélération ( m/s)
L'accélération est donc constante en valeur et dépend de la vitesse ainsi que du rayon de la trajectoire


Or d'après la 2nde loi de Newton : .

Avec : les forces extérieures exercées sur le satellite.

m: la masse du satellite.

: l'accélération du centre d'inertie du satellite.

Autre remarque : très bien aussi pour la qualité rédactionnelle de ton message du 26-08-20 à 10:31, c'est ce qu'il faudrait faire désormais pour toutes les questions des exercices pour lesquels tu as besoin d'aide : bien définir les notations employées, les hypothèses associées à une loi, etc.

Le vecteur accélération est un vecteur qui impose un changement de direction en tout point de la trajectoire.

Il est donc dirigé vers le centre ( à l'inverse du vecteur de position qui lui est dirigé vers le vecteur vitesse.

Pour la direction , c'est celui du rayon.

Pour plus de précisions , voici un schéma que j'ai essayé de faire à l'aide de GeoGebra.

Oui TB !

Et donc, qu'en est-il pour ?

Cela va te permettre de répondre à la question posée.

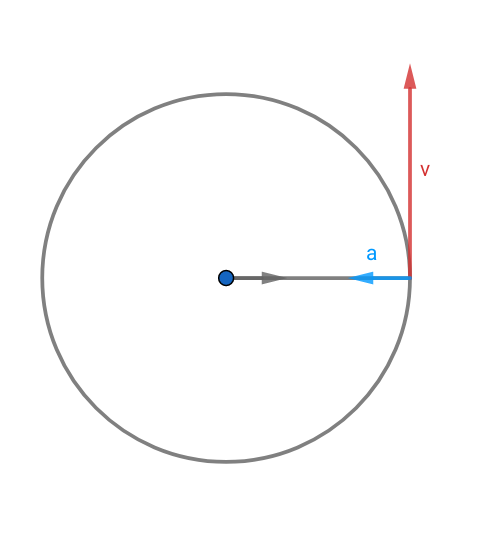
Cette somme algébrique est donc nulle car le vecteur accélération est perpendiculaire au vecteur vitesse (il est donc normal à ce vecteur et constant).

Et pour être plus rigoureux , ce vecteur est constant car il est caractérisé par sa direction, son sens et sa longueur (non nulle).

Non !

Souviens-toi de ce que tu as écrit plus haut :

Citation :
Or d'après la 2nde loi de Newton : .

Avec : les forces extérieures exercées sur le satellite.

m: la masse du satellite.

: l'accélération du centre d'inertie du satellite.

Ah , désolé..

Les caractéristiques de sont donc les caractéristiques du vecteur .

C'est l'idée mais pas tout à fait :
* même point d'application ;
* même droite d'action ;
* même sens ;
* mais pas la même valeur (cf. la relation écrite).

Tu es donc désormais en mesure de répondre à la question, non ?

Ah oui , car y a la masse qui multiplie cette somme algébrique..

Les bonnes réponses sont donc les réponses a et c.

OK.

2) Dans le référentiel héliocentrique, le centre de la Terre décrit un cercle autour du Soleil, ainsi que le centre de toutes les planètes de notre système solaire.

Par conséquent le satellite n'est soumis qu'à la force de gravitation attractive exercée par la Terre. La direction de cette force passe toujours par le centre de la Terre : il s'agit donc d'un champ de force centrale.


Ainsi les forces s'exerçant sont : Le poids du satellite et les forces de frottement . ().

Schéma :

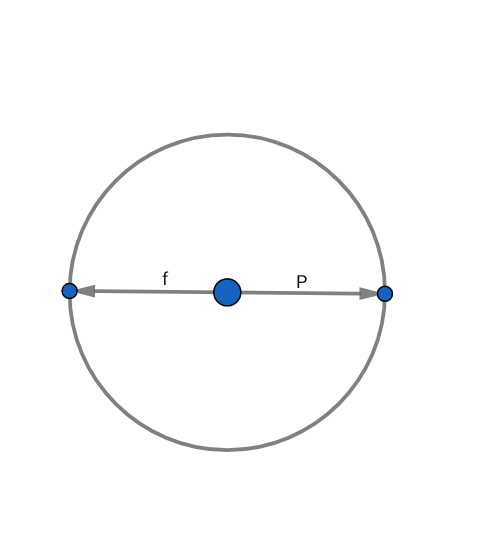
Bonjour kamikaz,

Tu es en train de me prouver que tu n'as pas lu attentivement la fiche que je t'ai fournie et que tu ne suis pas les conseils et rappels de cours fournis en question 1 :

* référentiel héliocentrique = référentiel ayant pour centre le Soleil.

Or l'énoncé te précise ceci :

Tu t'en sors ?

Quelques indications complémentaires :

Citation :
2) Étude d'un satellite de la terre.

2-1) Un satellite tourne autour de la terre à une altitude h , d'un mouvement circulaire uniforme.

2-1-1) Quel est le centre de la trajectoire ? Représentez sur un schéma , le (ou les) force(s) s'exerçant sur le satellite.

Question résolue, cf. message du 27-08-20 à 11:29

2-1-2) Déterminer l'accélération du mouvement du centre d'inertie du satellite en fonction de g₀ : intensité de pesanteur à la surface de la terre R_T : le rayon de la terre et h.

Il faut déjà commencer par exprimer la force d'attraction gravitationnelle d'un objet à la surface de la Terre :

F(objet) = ...

or à la surface de la Terre, cet objet est soumis à son poids P = m(objet)*g0

donc par analogie (en regardant les deux formules) : g0 = ?

Ensuite, si h est l'altitude du satellite depuis le sol de la Terre (c'est ce que je suppose, l'énoncé ne précise rien), d'après la deuxième loi de Newton, on a :

F(satellite) = m(satellite)*a(satellite)

si a(satellite) est son accélération

<=> G*m(satellite)*M(Terre)/(Rt + h)² = m(satellite)*a(satellite)

<=> a(satellite) en fonction de g0 exprimé plus haut.


2-1-3) Établir la relation : donnant la période de révolution en fonction de l'altitude h.

Tu sais que dans un mouvement circulaire uniforme, l'accélération du satellite peut s'exprimer sous la forme :

a(satellite) = v(satellite)²/(Rt + h)

or on a exprimé a(satellite) en fonction de g0 en question 2-1-2).

Conclusion ?

Oui , çà vient ..

Bonjour ,

_objet=m _objet× ==> .

*Au sol : (1)

*En altitude :

(2).

Le rapport de (2)/(1)=

Bonjour,

Oui c'est bien ça pour g0 !

Il te suffit de dérouler le raisonnement proposé ci-dessus pour parvenir aux relations demandées par l'énoncé.

Attention : la notion de poids d'un solide ne s'applique pas pour des altitudes trop élevées par rapport à la surface terrestre (ce qui est le cas du satellite)



***Mis à jour 28/08 11h13***

Bonjour,

Juste une remarque ....
Question 2.1.3
La relation à démontrer   n'est pas homogène. Elle est donc fausse.
Il s'agit probablement d'une mauvaise recopie de l'énoncé, mais il vaut mieux rectifier cette relation avant d'essayer de la démontrer.

Bonsoir odbugt1,

Oui, on allait finir par retrouver la bonne formule en déroulant la méthode

Je veille au grain cette fois-ci !

@kamikaz : je risque de mettre du temps à te répondre ces prochains jours mais je lirai ce que tu as fait dès que possible. Détaille bien ton raisonnement pour gagner du temps (hypothèses, phrases pour expliquer le raisonnement, schéma, ...)

Bonsoir,

J'ai beau faire , çà coince vraiment

Bonjour kamikaz,

Me revoici après quelques jours de déconnexion !

Pourrais-tu me détailler ce que tu as été en mesure de faire pour que je comprenne où tu coinces ?

Ok , je reviens !

2-1-3) On a montré que .

Le mouvement étant circulaire uniforme ,





(a désigne l'accélération)..

Bonjour kamikaz,

N'ayant pas trop été disponible ces derniers jours, je reprends un peu ce qu'on a fait plus haut pour me remettre à niveau :

Citation :
2-1-3) Établir la relation : donnant la période de révolution en fonction de l'altitude h.

v(satellite) =( g0 * Rt²/(Rt + h) )

T = 2*(Rt + h) / ( g0 * Rt²/(Rt + h) )]

J'ai simplifié mais je n'arrive pas à trouver la même chose ..

Souviens-toi qu'odbugt1 nous a alerté sur la non homogénéité de la formule proposée par l'énoncé (erreur de recopie ?).

D'ailleurs, tu peux faire entrer le terme (Rt + h) dans la racine pour simplifier la relation

Aucune erreur de recopie ..

Dans ce cas il y a une coquille dans l'énoncé, simplifie au maximum l'expression qu'on a trouvée et on en a fini avec la question.

Ok , pas de problème

Mais çà coincerait à la question 2-2-1 puisqu'on a vraiment besoin de cette formule pour vérifier la distance Terre-Lune ..

Pourquoi ?

Il suffit d'utiliser la formule qu'on a trouvée en 2.1.3 pour répondre à cette question.

Ce sera une bonne manière de vérifier si nous n'avons pas fait de faute d'inattention.

Attention à la rédaction, je pense que tu as fini par l'intégrer.

J'ai réussi , mais je n'arrive pas vraiment à saisir ce que j'ai fait au LaTex ..

Il est serait aussi illisible si je le fesais sans LaTex..

Même avec le bouton "assistant Latex" ?

Oui , j'aimerais bien faire une grande accolade fermante '' } ''

bonjour, je ne fais que passer...
pour avoir une grande fermante, il faut au départ une grande ouvrante, et la taille va s'ajuster automatiquement au contenu
\left\{ et \right\}

essai :

Bonsoir , bon j'ai tout fait mais je n'ai pas réussi vraiment à écrire ce que je voulais ..

Tant pis..

2-1-4) Le mouvement étant circulaire uniforme ,



2-2-1) (d_TL=R_T+h)

Pour les autres questions çà va ..

Merci beaucoup

odbugt1 avait raison ..

C'est

Je dirais plutôt :

Oui