Comment les  Egyptiens  hissèrent-ils d'énormes blocs de pierre au sommet des pyramides ?
Personne n'est vraiment sûr de la technique employée, mais ils se servirent très probablement de plans inclinés construits au fur et à mesure de l'élévation de la pyramide. Ils faisaient glisser les pierres le long de ces rampes, des rouleaux de bois intercalés entre le bloc et le plan rendaient les frottements négligeables. La force alors nécessaire à la traction des blocs était inférieure à leur poids. En revanche, la distance à parcourir sur le plan incliné était plus longue que s'ils avaient eu recours à un système de levage vertical.


1)Un homme seul hisse sur un plan incliné un bloc rocheux de masse m en le tirant avec une corde parallèle aux lignes de plus grande pente.
Le plan incliné est suffisament lisse pour qu'on puisse supposer des forces de frottement négligeable. il fait un angle avec le plan horizontal.
a-Quelle force de traction l'homme doit-il exercer sur la corde en supposant que la vitesse du bloc est constante ?
b-Exprimer le travail qu'il effectue pour un déplacement l le long  du plan incliné.
c-Exprimer en fonction de l et de la hauteur h dont s'est élévé le bloc rocheux.

J'aurais besoin d'aide s'il vous plait. Pourrais-je en meme temps savoir quelles sont les différentes forces de tractions qui existent et leur caractéristiques svp

Merci d'avance
Mini.  

*** message déplacé ***

Bonsoir,
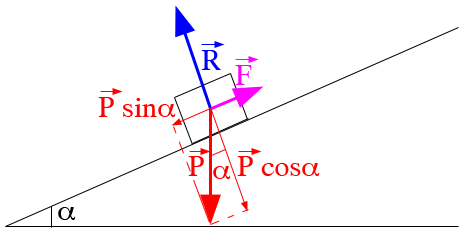
Si la vitesse est constante, la somme des forces est nulle (voir schéma)


En supposant l'axe du plan incliné orienté positivement vers le haut :

Ceci pour la réponse à la question 1a

Bonjour,

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
  
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
  
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Coll j'ai déjà regardé et ce n'est pas les même questions. Mais il existe plusieurs exercices avec ce nom.

Merci Marc35, j'ai enfin compris et j'ai donc pû en déduire la suite

mini >>

Tu as posté deux fois le même exercice, dans deux topics différents, le 28 décembre, une fois à 22 h 08 et une fois à 22 h 16
C'est exactement cela le multi-post qui n'est pas toléré dans ce forum.
 

Bonjour tout le monde,
j'ai un ptit exercice pour les vacances mais je n'arrive pas à placer mes forces donc je ne peux pas  continuer mon exercice. Si quelqu'un pourrais m'aider ça serait sympa de sa part

Alors voilà l'énoncé, c'est la question 2 que je n'arrive pas. La 1 étant déjà faite je ne la poste pas :


Avec un système de levage :

4 hommes hissent verticalement à vitesse constante le même bloc rocheux d'une meme hauteur h (h=Pcoscarré (+90) x l d'après le c) de la Q1).
a-Quelle est l'expression de la force de traction qu'ils doivent exercer sur la corde ?
b- Chaques hommes exercent la même force de traction que l'homme de la Q1(avec un plan incliné mais on n'avais pas de valeurs donc on trouver : Fsupérieur à mgcos (+90) ). En déduire la valeur de l'angle formé par le plan incliné avec l'horizontal.

Merci. Si vous avez besoin de la Q1 je vous l'écrirai mais je ne pense pas que ce la soit utile. Voilà merci d'avance

*** message déplacé ***

Bonjour,

extrait de la FAQ du forum :

Q04 - Où dois-je poster une nouvelle question ?

Pour poster un nouveau message, choisissez le forum correspondant à votre niveau : collège ou lycée ou supérieur.

Pour parler du site en général (forum, suggestions d'amélioration, problème rencontré avec une fonctionnalité, etc.) utilisez plutôt le forum site.

Il existe également des forums plus spécifiques : Autre, Détente, Expresso, Espace Profs, etc.

Une fois le bon forum trouvé, choisissez "Nouveau sujet" ou descendez sous la liste des messages pour avoir accès au formulaire " Poster un nouveau message ". Et remplissez soigneusement les différents champs en respectant les consignes de bon usage que vous pourrez trouver tout au long de la lecture de cette F.A.Q.

Après les conseils de Coll, pour "enfoncer encore le clou"... mini, ouvre un nouveau topic avec ton nouvel exercice en entier. C'est plus facile pour ceux qui essaient de t'aider...
Et tu mets tes réponses... enfin celles que tu as réussies à trouver.

Comme tu en as déjà écrit une partie, utilise le copier-coller et complète...

Je n'ai pas tout compris...
Tu as ouvert un autre topic avec la deuxième question du même exercice.
Pourquoi ne l'as-tu pas mis à la suite tout simplement ?

Mets donc tes réponses pour 1a, 1b, 1c parce que

Citation :
h=Pcoscarré (+90) x l d'après le c) de la Q1

alors pourquoi j'ai pas fais copier/coller pck j'ai de gros problème internet et donc bah ça beug énormément.
Coll t'es maisons je les vois pas désolée :s je reçois mal la connexion...désolée


Alors sinon pour la question j'ai refais mon exercice et je m'étais totalement trompé donc voilà mes nouvelles réponses:

1a) F=-Psin
1b)W= F x l x cos
        =-Psincos x l

1c) je ne trouve pas.


encore désolée pour la connexion internet et pour tous les problèmes que je cause :s

Euh non je trouve F=Psin pour la 1a)
Mais je comprend pas pourquoi tu dis que F=-Psin alors que -Psin+F = O
normalement si je suis ton résonnement, -Psin=-F d'ou F=Psin. non?

Donc la 2b) change je trouve alors W=F x cos x l
                                                          = Psincos x l

1b) Le déplacement étant l, le travail est  
1c)
2a) La force de traction est  
2b) L'homme de la question exerce une force  .
Donc on a  

Peux-tu trouver sin et ?

Dans 1c, j'ai dit une bêtise :
1c)  

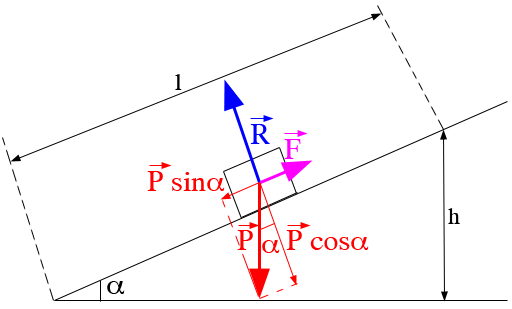
Dans 2a, j'ai peut-être été un peu rapide...
La vitesse étant constante, la somme des forces est nulle donc :

Par projection sur un axe vertical orienté vers le haut :

Merci Marc35!!!!

Grâce à toi j'ai compris, parce que j'ai refais mon exercice sans regarder ici et j'avais les même réponses que toi
Tu m'as été d'une grande aide merci beaucoup.

Et encore désolée pour tous les problèmes que j'ai eut avec mon internet.

Je trouve donc pour sin = 1/4  d'où =14,5° (en arrondissant)
  

OK pour 14,5°...
Pour les problèmes Internet, ça arrive à tout le monde. C'est mon cas en ce moment aussi...