Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

la célérité d'une onde ultrasonore dans un liquide

Posté par
Physical111 20-10-20 à 16:32

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
Les ondes mécaniques se propagent Seulement dans un milieu matériel, et leur célérité croit avec la densité du milieu où elles se propagent
Partie 1 : question de cours
1-1 Répondre par Vrai ou faux:
a-les ondes sonores  sont des ondes mécaniques ==> vrai
b- les ondes ultrasonores  sont des ondes électromagnétiques
==> Faux
C) les ondes ultrasons ne se propagent pas dans le vide
==> Vrai
D) le phénomène de diffraction ne peut pas être obtenu par les ultrasons
==> Vrai
E) les ondes ultrasonores se propagent dans l'air avec une vitesse égale à la célérité de la lumière c
=> Faux
partie 2: célérité d'une onde ultrasonore dans le pétrole
Pour déterminer la valeur approximative de la célérité vp d'une onde ultrasonore dans le pétrole liquide ,on réalise l'expérience suivante ;
Dans une cuve contenant du pétrole, on fixe à l'une de ses extrémités deux émetteurs E1 et E2 qui sont reliés à un générateur GBF . À l'instant t0=0 , les deux émetteurs émettent chacun une onde ultrasonore , une se propage dans l'air et l'autre dans le pétrole . Les récepteurs sont à une distance L des émetteurs (voir figure 1)
On visualise sur l'écran d'un oscilloscope les deux signaux reçus par R1 et R2 (voir figure 2)
*Données
- les deux ondes parcourent la même distance L=1,84 m
- la célérité des ultrasons dans l'air Vair= 340 m/s
- la sensibilité horizontale de l'oscilloscope Sh=2ms/div
2-1 on exploitant la figure 2 , déterminer la valeur du retard temporel entre les deux ondes reçus
2-2 montrer que L'expression de s'écrit sous la forme :

={\color{red}{\huge L×[\dfrac{1}{V_a_i_r}-\dfrac{1}{V_p}]}}
2-3 trouver la valeur approchée de la célérité Vp
J'ai répondu à la question de la partie 1 tous (cf en haut)
Il me reste la partie 2
Une petite indication s'il vous plaît pour la question 2-1 merci beaucoup d'avance

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 20-10-20 à 16:46

Bonjour
2-1) =2×2=4 ms =4×10-3 s
2-2 j'ai aucune idée , une petite indication s'il vous plaît merci beaucoup d'avance
Merci beaucoup d'avance

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 20-10-20 à 21:12

Bonjour à tous ,
Rectification pour la réponse à la question 1-1 partie 1
a- vrai , b- faux , c- vrai , d- faux , e- faux
Partie 2
2-1) déjà abordé
2-2) on a = t2- t 1
• t2 est la durée de propagation dans l'air
D'où on a Vair=L/∆t<=>∆t=L/Vair
Avec ∆t=t2- t0=t2
• t1 est la durée de propagation dans le pétrole
D'où on a Vp=L/∆t<=> ∆t=L/Vp
Avec ∆t=t1-t0=t1
D'où =L(\dfrac{1}{V_a_i_r}-\dfrac{1}{V_p}
2-3) on a
=L(\dfrac{1}{V_a_i_r}-\dfrac{1}{V_p}
Je vais noté : z
Z- \dfrac{L}{V_a_i_r} = - \dfrac{L}{V_p}<=> \dfrac{1}{L}( Z-\dfrac{L}{V_a_i})=-\dfrac{L}{V_p}×\dfrac{1}{L} <=>\dfrac{Z}{L}-\dfrac{L}{L×V_a}=-\dfrac{1}{V_p}<=> V_p×\dfrac{1}{V_p}=(\dfrac{1}{V_a}-\dfrac{Z}{L})V_p <=>1=\dfrac{V_p}{V_a}- V_p \dfrac{Z}{L}<=> 1=V_p( \dfrac{1}{V_a}-\dfrac{Z}{L})
D'où
\boxed{V_p=\dfrac{1}{\dfrac{1}{V_a_i_r}-\dfrac{Z}{L}}}
Merci beaucoup

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 21-10-20 à 14:04

Bonjour
Est ce qu'il y a une Réponse ?

Merci beaucoup

Posté par
athrunre : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 09:07

Bonjour Physical111,

Ok pour ta rectification de la question 1-1.

Peux-tu uploader les deux images de l'exercice ?

Je suis d'accord avec ta réponse à 2-2. Pour être encore plus rigoureux, il faudrait nommer les "\Delta t" différemment pour la propagation dans l'air et la propagation dans le pétrole :

(\Delta t)_1=t_1-t_0=t_1=L/v_p
(\Delta t)_2=t_2-t_0=t_2=L/v_\mathrm{air}

\tau=(\Delta t)_2-(\Delta t)_1=t_2-t_1=\dfrac{L}{v_\mathrm{air}}-\dfrac{L}{v_p}
\boxed{\tau=L\left(\dfrac{1}{v_\mathrm{air}}-\dfrac{1}{v_p}\right)}

Je n'ai pas compris ta phrase "je vais noter : z" ? J'ai l'impression que tu as remplacé \tau (tau, \tau en \LaTeX) par Z.

Sachant qu'on connait la valeur du retard \tau via la figure 2, il suffit effectivement d'isoler v_p dans la formule encadrée ci-dessus, ce que tu as fait correctement

J'attends que tu uploades les figures pour pouvoir vérifier les valeurs numériques.

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 09:31

Bonjour
Merci beaucoup de m'avoir répondu !
Je suis tellement désolé j'ai pas uploader l'image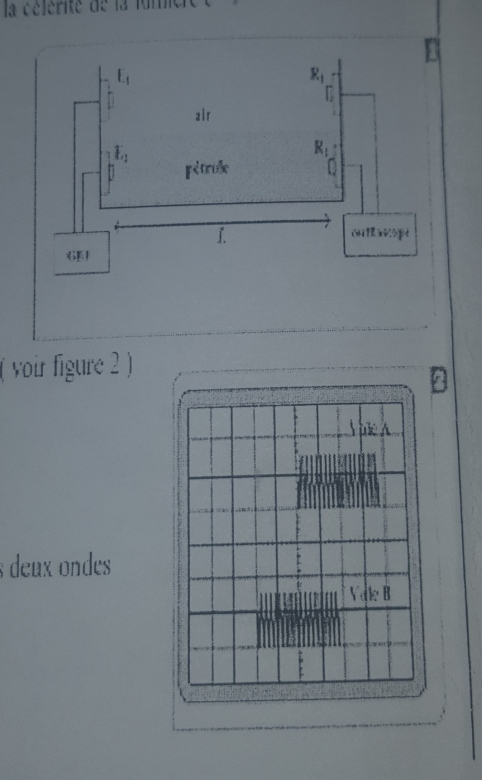 la célérité d\'une onde ultrasonore dans un liquide
Désolé ce n'est pas en bonne qualité

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 09:37

Citation :
J'ai l'impression que tu as remplacé \tau (tau, \tau en \LaTeX) par Z.

Oui exactement .

Posté par
athrunre : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 09:47

Donc effectivement, on constate un retard égal à deux divisions sur la figure 2, ce qui correspond à 2\times2=4\ \mathrm{ms}.

La voie A correspond au récepteur R1 (air) et la voie B au récepteur R2 (pétrole). Le récepteur R2 reçoit un signal avant R1 car notre onde sonore se propage plus rapidement dans le pétrole que dans l'air, la raison étant que le pétrole est plus dense que l'air.

Grâce à la formule

v_p=\dfrac{1}{\dfrac{1}{v_\mathrm{air}}-\dfrac{\tau}{L}}

tu peux calculer la célérité v_p.

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 10:01

Bonjour
Merci beaucoup de m'avoir répondu !
v_p=\dfrac{1}{\dfrac{1}{v_\mathrm{air}}-\dfrac{\tau}{L}}
Donc A.N
Vp=\dfrac{1}{\dfrac{1}{340}-\dfrac{4×10^{-3}}{1,84}}=1303,3m.s^{-1}

Posté par
athrunre : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 10:06

C'est juste !  Comme tu peux le constater la célérité du son dans le pétrole (milieu liquide) est bien supérieure à celle dans l'air (milieu gazeux, bien moins dense).

Posté par
Physical111re : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 10:08

Merci beaucoup à vous
Vair=340 m s-1
V pétrole=1303,3 m.s-1
D'où Vp>Vair

Posté par
athrunre : la célérité d'une onde ultrasonore dans un liquide 22-10-20 à 10:34

Oui !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !