Inscription / Connexion Nouveau Sujet
IPhO Ressort
Bonsoir,
Il y a une question à un QCM des IPhO 2017 auquelle je bloque. La voici :
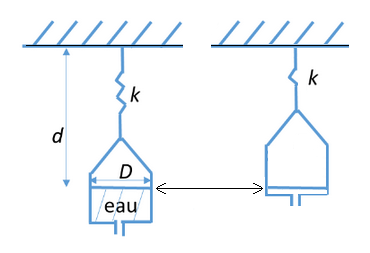
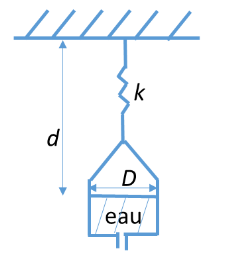
Q.18 (*) Un cylindre ouvert de diamètre D = 30 cm contient de l'eau, de masse volumique 1000 kg.m-3 .
Ce cylindre est accroché via un ressort de raideur k à une paroi horizontale fixe.
L'eau peut s'évacuer par un trou placé à la base du cylindre.
Quelle valeur donner à k pour que la distance d entre la surface de l'eau et la paroi horizontale soit maintenue constante (on prend g = 9,81 m.s-2) ?
(a) 3,4.102 N.m-1
(b) 2,7.103 N.m-1
(c) 6,9.102 N.m-1 (c'est la bonne réponse)
(d) 1,7.102 N.m-1
Mais pouvez-vous m'expliquer pourquoi svp ?
Mais d'abord, je vous explique ce que j'ai fait :
Ma 1ère idée est :
La vitesse d'écoulement de l'eau est m.s-1 (vue dans le cours)
La masse de l'eau serait : Peau = pi x 0,152 x 0,3 = 2,426 kg
Par analyse dimensionnelle, on trouverait que la vitesse du ressort est : <-->
N.m-1 ce qui correspondrait à la réponse (a)
Ma 2nd idée est :
m.s-1
(avec d que je dis égal à 0,6m en mesurant à la règle

 ) ce qui correspond bien à la réponse (c) en remplaçant k par 6,9.102
) ce qui correspond bien à la réponse (c) en remplaçant k par 6,9.102
Je suis sûr que mon 2ème résonnement est archi faux mais je vous le transmets quand même.
Merci d'avance 
Soit ΔF la variation du module de la force exercée par le ressort : ΔF = k* Δx
Soit ΔP la perte de poids du système : ΔP = ρeau * S * Δx * g (même Δx pour que d reste constant)
ΔF = ΔP
k = ρeau * S * g = 1000 * (π*0,3²/4) * 9,8 = 6,9.102 N/m
Merci beaucoup pour ta réponse odbugt1 
Mais S, qui représente le volume du cylindre, tu l'exprime par :
π*0,3²/4
Tu insinues donc que la hauteur du cylindre vaut 0,4m. Mais qu'est-ce qui te permet de dire ça ? Est-ce une approximation de ta part ?
Tu insinues donc que la hauteur du cylindre vaut 0,4m. Mais qu'est-ce qui te permet de dire ça ? Est-ce une approximation de ta part ?
Je "n'insinue" rien, je ne fais aucune approximation non plus.
Je m'en tiens à l'énoncé qui note " D " le diamètre ( et non la hauteur) du cylindre.
Reprenons :
Soit ΔP la perte de poids du cylindre d'eau : ΔP = ρeau * S * Δx * g
Si tu fais une analyse dimensionnelle tu te rendras compte que S a la dimension d'une aire et non d'un volume.
S est l'aire circulaire de la surface libre du cylindre et, comme chacun le sait une l'aire d'un disque de diamètre " D " peut se calculer par la relation : S = πD²/4
OK
Justification un peu plus détaillée :
A gauche : P = T ( Ce sont les modules du poids et de la tension du ressort )
A droite : P' = T'
P-P' = T-T'
ΔP = ΔT
ρeau * S * |Δx1| * g = k |Δx2|
|Δx1| = |Δx2| puisque d reste constant.
k = ρeau * S * g