Inscription / Connexion Nouveau Sujet
Induction électromagnétique 2
Bonjour, Encore besoin de votre aide pour ce sujet. Merci
ÉNONCÉ
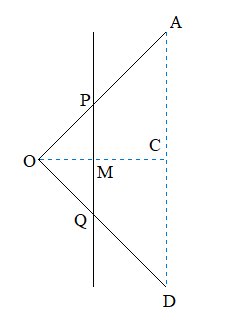
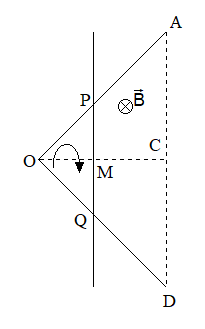
Deux tiges (OA) et (OD) sont soudées et forment un angle droit en O. OA = OD = ⍺ = 0.8m. Une autre tige (PQ) de même nature et de même section que (OA) et (OD) se déplacent parallèlement à (AD), avec une vitesse constante . Soit le point C, milieu de (AD) et M le point d'intersection de (PQ) avec l'axe (OC). La position de la tige (PQ) est repérée depuis le point O par OM = x, le déplacement s'effectuant jusqu'en C. On donne μ, la résistance linéique des tiges (OA), (OD) et (PQ).
On donne μ= 1.24 Ω/m; B=0,12T; v=0,65m/s
1/ 1.1 Exprimer la surface balayée (ou surface du circuit) en fonction de x.
2. En déduire l'expression du flux magnétique.
3. Donner l'expression de la f.é.m. d'induction.
4. Donner l'expression de l'intensité induite du courant et calculer sa valeur
Dans le prochain message je donne mes pistes de réflexions.
La question 1 relève de la géométrie et ne présente pas de difficulté.
Les questions 2 et 3 sont des applications immédiates du cours.
L'un n'empêche pas l'autre .....
Et comme la question porte sur l'aire du triangle OPQ il est plus efficace d'utiliser PM = OM
Oui je viens de voir POM(angle)=π/4
Donc on a bien un triangle rectangle isocèle en M POM
Donc si je continue
S =2PM*x / 2 or PM =OM = x
Au final j'obtiens S=x²
Le sens de dépend de l'orientation qu'on choisit sur le circuit.
Pour simplifier, compte tenu que dans cet exercice les signes algébriques du flux magnétique et de la fém d'induction sont d'importance secondaire je suggère :
|Φ| = B.S = B.x²
de manière à ne manipuler que des grandeurs positives
La tige PQ se déplace à la vitesse v :
x = v * t
|Φ| = B * x² = B * v² * t²
|e| = |- dø/dt| = ........
Je te laisse continuer
c'est un peu bizarre avec les valeurs absolues
On ne peut plutôt pas orienter et
dans le même sens ?
Oui, tu peux orienter le circuit électrique de manière que et
soient de même sens.
Tu auras alors :
Φ = B * x²
et e = - 2 B * v² * t
Autre possibilité :
Tu orientes le circuit de manière que et
soient de sens contraires.
Dans ce cas
Φ = - B * x²
et e = 2 B * v² * t
Fais comme tu le préfères.
enfin le dernier :4. Donner l'expression de l'intensité induite du courant et calculer sa valeur
on a i = e/R or ici R =µl avec l = 0P + PM + MQ + QO
l = 2PM + 2OP
l = 2x + 2x 2
2
l = 2vt + 2vt 2
2
donc
OK.
Il te faut alors préciser que tu as orienté le circuit dans le sens OPMQ ce qui implique un vecteur dans le même sens que
OK pour l'expression de i
Sa valeur négative indique que le courant circule en sens inverse du sens positif choisi ce qui est conforme à la loi de Lenz.
Il ne te manque plus que l'application numérique.
OK pour l'expression de i
Sa valeur négative indique que le courant circule en sens inverse du sens positif choisi ce qui est conforme à la loi de Lenz.
Il ne te manque plus que l'application numérique.
i=-2,61.10^-2