Bonjour
Dans sa région centrale, le solénoïde peut être assimilé à un solénoïde infiniment long. Tu peux donc déterminer l'expression du vecteur champ qu'il crée lorsqu'il est parcouru par un courant d'intensité I1. Calcule alors le flux de ce vecteur champ à travers la bobine.
Important : faire un schéma en vue de dessus précisant clairement les orientations du solénoïde et de la bobine ainsi que les vecteurs utiles.

On demande une inductance "MUTUELLE". C'est ma première fois d'entendre ça dans un exercice.
Cette inductance mutuelle est-elle la somme des inductance de chaque bobine ?

Rien d'étonnant. Cette notion n'est pas au programme de la plupart des classes de terminale,sauf quelques filières technologiques.
En quelques mots : soit une bobine ou solénoïde n°1 parcouru par un courant d'intensité i1 créant un champ magnétique de vecteur . On peut définir le flux de ce vecteur champ à travers une bobine n°2 : ₂. Dans la mesure où B₁ est proportionnel à i₁, le flux magnétique ₂ est aussi proportionnel à i ₁. On pose :
₂ = M.i₁ où M est appelée inductance mutuelle, grandeur dépendant des deux bobines ou solénoïdes et de leurs positions relatives.

J'adopte les notations suivantes :
• pour le solénoïde n⁰1 :
- surface d'une spire : S₁ = 8 cm² ;
- nombre de spires par unité de longueur : n₁=20spires/cm ;
- champ magnétique B₁ créé par le courant i₁

• pour la bobine n⁰ 2 :
- surface d'une spire : S₂ ;
- nombre de spires par unité de longueur : n₂ ;
- nombre de spires N₂ = 40 spires
- champ magnétique B₂ créé par le courant i₂

Selon ce que j'ai compris de ton explication, le flux du champ magnétique B₂ à travers le solénoïde est :



Or B₁ = ₀n₁i₁

Donc



Alors l'inductance mutuelle est :



Dans l'expression de l'inductance mutuelle, S₂ est inconnu. Impossible de faire l'application numérique. Ni le rayon, ni le diamètre de la bobine n⁰2 n'est donné. Impossible de déterminer la surface S₂.

Soit une section de la bobine n° 2 d'aire S2. Le champ créé par le solénoïde est uniforme à l'intérieur de ce solénoïde et nul à l'extérieur du solénoïde. Donc le flux de B1 est non nul uniquement à travers le disque d'aire S1.

Donc S₂ = S₁

Donc on s'intéresse uniquement à la partie située à l'interieur du solénoïde n⁰1. La section est S₁

Alors

D'accord !

AN :  M = 8,04.10^-5 H

OK ! sous réserve que le sens de circulation positif dans la bobine soit choisi identique à celui correspondant à un courant d'intensité positive dans le solénoïde. Sinon on obtient : M= -8,04.10^-5H. Contrairement à auto-inductance L qui est toujours positive, la mutuelle inductance M possède un signe qui dépend des choix d'orientations des deux bobines ou solénoïdes.
La suite est facile...

D'accord !

J'ai une question.
Ici, comme expliqué dans ton message du 12-04-24 à 16:38, le flux du champ B1 à travers la bobine n⁰2 est ₂ = Mi₁

Est-ce qu'on pouvait passer aussi par le flux du champ B2 à travers la bobine n⁰1 et trouver l'inductance mutuelle, en posant que : ₁ = Mi₂  ?
Obtiendrait-on le même résultat ?

J'ai du mal à faire un dessin soigné de la situation. Aidez-moi svp.

On démontre au niveau (bac+2) voire plus, que les deux méthodes conduisent au même résultat pour M. Au niveau terminale, cela peut se vérifier en imaginant deux enroulements de fils très fins sur un même cylindre de longueur très grande devant le rayon.. Pour la figure, tu peux choisir comme plan de figure un plan perpendiculaire à l'axe de symétrie commun à la bobine et au solénoïde.

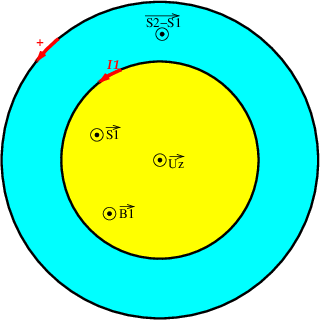
Exemple de schéma où est un vecteur unitaire dirigeant l'axe (O,z), axe de symétrie commun à la bobine et au solénoïde.

Merci bien.

Question b)
Par définition :

Or le flux est = Mi

Donc  

AN : e = 4,02.10^-4 V

D'accord avec toi !

Merci bien